Исследовательская работа "Геометрические головоломки". Головоломка из геометрических фигур

Новый: Игры

Вы любите играть?

Значимость и незаменимость игры в нашей жизни давно уже доказана многими психологами, учеными и самой жизнью. Мы играем с самого детства, учимся общаться в процессе игры, строить отношения.Собраться всей семьей или с друзьями, поболтать о разном, угостить всех чем-нибудь вкусненьким, сыграть несколько увлекательных партий в настольную игру – все это то, что придает нашей жизни особый колорит. Сегодня увлечение настольными играми принимает тотальный характер. Ведь современные настольные игры – это не только «бродилки», но и стратегические, экономические, детективные, логические игры. В мире существует уже до 10 тысяч настольных игр разной тематики. Конечно, за всеми новшествами не угнаться, а некоторые игры слишком дорого стоят. Но ведь игру можно сделать и своими руками Вот несколько игр.

Танграм

Игры-головоломки, на воссоздание из геометрических фигур образных изображений используются для совершенствования зрительного восприятия, и анализа, зрительной памяти, комбинаторики. Наборы фигур представляют собой части разрезанной определенным образом фигуры: квадрата, прямоугольника, круга или овала. Они интересны детям. Детей увлекал результат - составить увиденное на образце или задуманное. Успешность освоения игры у детей зависит от сенсорного развития детей. Дети называли геометрические фигуры, их свойства, их отличительные признаки, свободно перемещать фигуры. У детей развивается умение анализировать изображения, выделять геометрические формы, видоизменять фигуры путем разрезания и составлять их из частей. Существуют различные игры- головоломки, на воссоздание из геометрических фигур плоскостных изображений предметов, животных, птиц, домов, кораблей такие как: «Танграм», «Пифагор», «Сфинкс», «Волшебный круг», «Колумбово яйцо», «Листик», «Вьетнамская игра», «Пентамино».

Но мы сейчас рассмотрим только одну из них - "Танграм".

Появление этой китайской головоломки связано с красивой легендой. Почти две с половиной тысячи лет тому назад у немолодого императора Китая родился долгожданный сын и наследник. Шли годы. Мальчик рос здоровым и сообразительным не по летам. Одно беспокоило старого императора Мальчику доставляло большое удовольствие целый день забавляться игрушками. Император призвал к себе трех мудрецов, один из которых был известен как математик, другой прославился как художник, а третий был знаменитым философом, и повелел им придумать игру, забавляясь которой, его сын постиг бы начала математики, научился смотреть на окружающий мир пристальными глазами художника, стал бы терпеливым, как истинный философ, и понял бы, что зачастую сложные вещи состоят из простых вещей. Три мудреца придумали "Ши-Чао-Тю" - квадрат, разрезаннный на семь частей.

Говорят, что танграм был любимой игрой Наполеона, который, лишившись трона, в изгнании проводил долгие часы за этой забавой, «упражняя свое терпение и находчивость»

Суть игры заключается в том, чтобы на плоскости из семи частей квадрата создавать самые разнообразные фигуры, силуэты предметов по образцу или замыслу. В коммерческих наборах обычно прилагаются карточки с заданиями.

1 вариант: Самый простой. Если ребенок маленький предложите ему составить фигуру путём наложения элементов на образец разделенными на составные части.

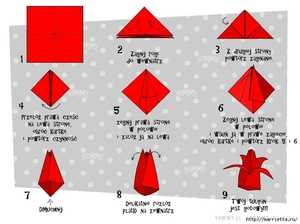
2 вариант: Если с первым разобрались ,то можно составлять фигуры по примеру, то есть картинка перед вами а элементы составляете уже смотря на фигуры разделённую на части.3 вариант: Для детей постарше, можно оставлять в фигуре только контуры.4 вариант: Собственно творческие задания - самому придумать и сложить фигуру.

Малыши тоже могут приобщаться к головоломке. Для них можно придумать совсем простенькие задания. Например, сложить из двух треугольников или из двух прямоугольников - квадратики, из треугольников - большой треугольник или параллелограмм. Таким методом можно изучить основные геометрические фигуры.

Сделать танграм можно самому. Это очень просто. Вам понадобятся шаблон головоломки. Распечатайте Танграм или нарисуйте сами по образцу. Можно использовать разноцветные элементы, если ребёнок маленький - заодно вспомните цвета, да и интереснее работать - играть с красочным

материалом.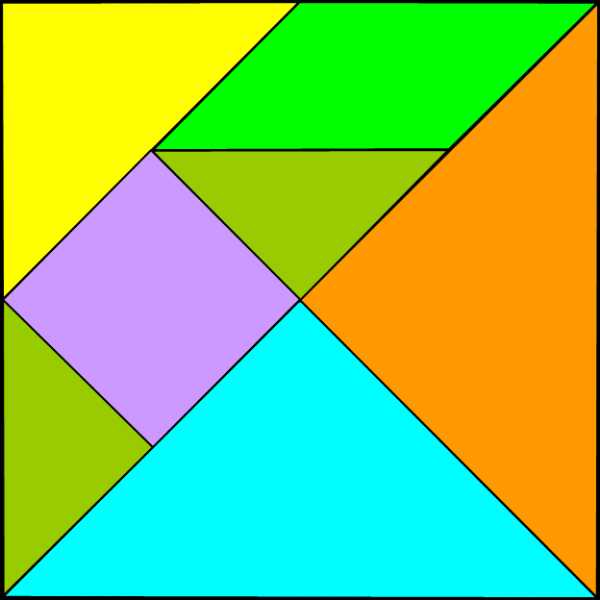

При решении головоломки требуется соблюдать два правила: первое — необходимо использовать все семь фигур танграма, и второе — фигуры не должны перекрываться друг другом. Взяв на вооружение математическую науку – комбинаторику, было получено более 5000 возможных вариантов сложенных фигурок.

Примеры сборки :

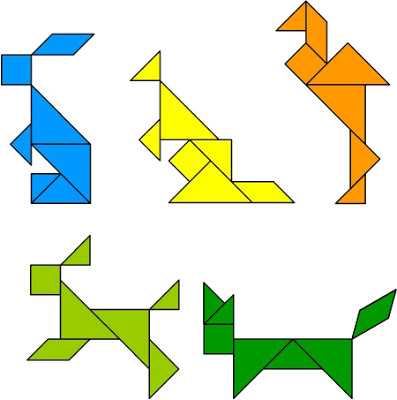
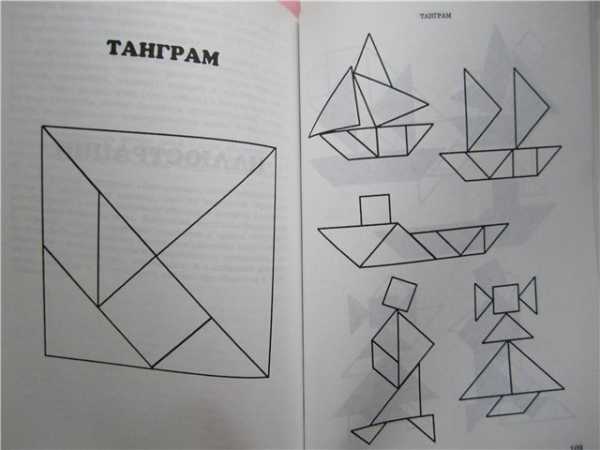
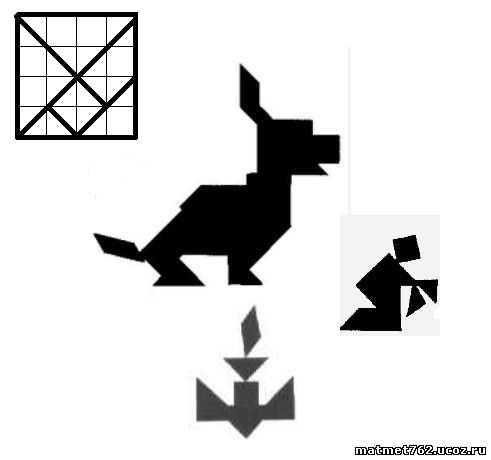
"ПИФАГОР"

Головоломка Пифагор очень похожая на старый добрый Танграм. Головоломка имеет форму квадрата, разрезанного на 7 частей, комбинируя которые, можно создать огромное количество геометрических фигур, силуэтов животных, людей, разных предметов и т.п. Все детали разного размера, в этом и заключается сложность, поэтому сложить фигуру из них достаточно сложно.

В инструкции к головоломке предлагаются 15 разных заданий. Головоломку Пифагор можно использовать на занятиях по математике, дома или в школе, ведь она отлично способствует развитию воображения, логики, внимания, пространственного мышления, математических и творческих способностей. Вы можете сделать из картона или вырезать из пластика головоломку Пифагор и Вашей семье гарантированы положительные эмоции и хорошее нестроение.

ВОЛШЕБНЫЙ КВАДРАТ

Геометрическая головоломка Волшебный квадрат относится ко второму уровню сложности и подходит для детей в возрасте от 4 лет. Занимаясь с головоломкой, ребенок познакомится с простыми геометрическими фигурами: треугольником, трапецией, квадратом.

Головоломка “Монгольская игра”

Разновидность геометрической головоломки, на подобии “Танграма” или “Квадрата Пифагора”.

Головоломка представляет собой квадрат разрезанный на 11 частей: 2 квадрата, один большой прямоугольник, 4 маленьких прямоугольника, 4 треугольника. Лучше всего изготовить такую головоломку из двустороннего картона или пластика.

Суть игры - собирать фигурки из данных элементов по принципу мозаики.

Как можно играть:

Составлять геометрические фигуры по образцу. В интернете можно найти готовые задания с ответами,, а можно придумать задания для своего ребенка и самим.Для того, чтобы нарисовать фигуры Вам потребуется лист в клетку. Можно взять обычный лист из школьной бумаги. Элементы из которых состоит “Монгольская игра” очень просты, и вам не составит большого труда составить из них композиции.

Вот, для примера, несколько фигур, составленных их элементов головоломки.

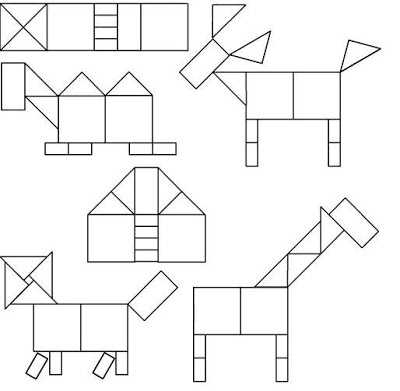Если ребенок маленький, то можно составлять фигуры по примеру, то есть фигурам, разделенными на составные части. Для детей постарше, можно оставлять в фигуре только контуры.

Головоломка "СФИНКС"

Головоломка «Сфинкс» состоит из разнообразных геометрических фигур: из4 треугольников и 3 четырехугольников с разным соотношением сторон. Из элементов можно собрать силуэты птиц, человека, животных, развивая наблюдательность и геометрическое воображение. Инструкция содержит схемы для построения более двух десятков фигур:

Игры - головоломки развивают пространственное воображение, комбинаторные способности, сообразительность, смекалку, находчивость. Простые в понимании, но достаточно трудные в решении, головоломки находятся на тонкой грани, соединяющей увлекательную игру и интеллектуальное развитие.

Головоломки от Алексея Шамшина

И ещё одна

Головоломка Архимеда СТОМАХИОН

Предлагаемая головоломка Архимедова игра — уникальный геометрический конструктор, в который играли еще в глубокой древности. Ее иное название "Стомахион".

Элементы игры получаются путем произвольного деления прямоугольника на 14 частей. Из получившихся деталей конструируют на плоскости разнообразные предметные силуэты, например, сидящей собаки, бегущего человека, разнообразных цветов, птиц. Можно сложить и многофигурные композиции. Знакомить ребенка с игрой необходимо постепенно.

Поупражняйте малыша в различении геометрических фигур. Можно предложить ребенку сосчитать стороны, углы, сгруппировать фигуры по форме, размеру, назвать их. Затем попробуйте конструировать простейшие изображения. Для облегчения головоломки Архимедова игра, предлагается сначала выкладывать фигуры по прилагаемым схемам.

Головоломка "ЛИСТИК"

Геометрическая головоломка-мозаика Листик разработана для детей в возрасте от 4 лет Фигура, напоминающая лист сирени. Этот лист сирени выложен из других фигур: треугольников, квадратов, трапеций.

Работа с головоломкой развивает глазомер ребенка, восприятие им формы, зрительно-моторную координацию, пространственное мышление и воображение. Способствует развитию произвольности (умения играть по правилам и выполнять инструкции), познавательной активности, мелкой моторики, воображения, сформированности сенсорных эталонов цвета, величины и формы, комбинаторных способностей, абстрактного мышления.

"Волшебный круг"

Круг разрезается на 10 частей. Правила игры те же, что и в других подобных играх: использовать для составления силуэта все 10 частей, не накладывая одну не другую. Разрезанный круг должен быть окрашен одинаково, с двух сторон.

ВЬЕТНАМСКАЯ ИГРА

В состав "Вьетнамской игры" входит разделенный на семь частей круг и рамка, в которую укладываются элементы. Все детали головоломки имеют обтекаемую форму, некоторые из них одинаковы по размеру. Предложите малышу сконструировать из замысловатых деталей силуэт какого-нибудь животного или птицы. Сначала можно задействовать не все элементы, затем постепенно усложнять задания.

Можно конструировать по схемам, а можно выдумывать свои сюжетные композиции.

Конструируя простые образные фигуры, дети учатся восприятию формы, способности выделять, фигуру из фона, выделению основных признаков объекта. Головоломка развивает глазомер, аналитико-синтетические функции, воображение (репродуктивное и творческое), зрительно-моторную координацию, умение работать по правилам. Игра предназначена для детей от 4 лет

КОЛУМБОВО ЯЙЦО

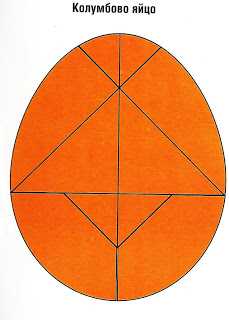
Существует рассказ - может быть, и вымышленный. Открыватель Америки Колумб был приглашен к всемогущему кардиналу Мендозе. За столом, по просьбе гостей, он начал рассказывать, как именно был им открыт Новый Свет (который, впрочем, он считал Индией). Кто-то из присутствующих, человек ограниченный, но самоуверенный, пожав плечами, сказал: «Так просто всё?»

Колумб взглянул на него и протянул ему лежавшее на блюде куриное яйцо: «Сделайте так, чтобы оно стояло на своем носке». Разумеется, попытки установить яйцо успехом не увенчались. «Это немыслимо...» - сказал обескураженный собеседник Колумба. «Это очень просто!» - с усмешкой ответил мореплаватель и, разбив о стол носок яйца, без труда заставил его стоять.

Выражение «колумбово яйцо» - стало воплощением остроумного и неожиданного выхода из затруднения, синонимом простого разрешения трудных вопросов.

Знакомимся с увлекательной головоломкой Колумбово яйцо, которая отлично скрасит время в дороге, ожиданиt в поликлинике и конечно же, разовьет логику и мышление ребенка. Принцип игры прост. Разрезаем по линиям фигурку яйца на мелкие детали. Задача ребенка – собрать фигурку по образцу. Но иногда можно пофантазировать и придумать свои варианты, разглядеть в фигуре знакомый образ.

Вот фигуры с заданиями

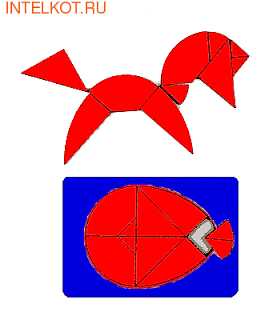
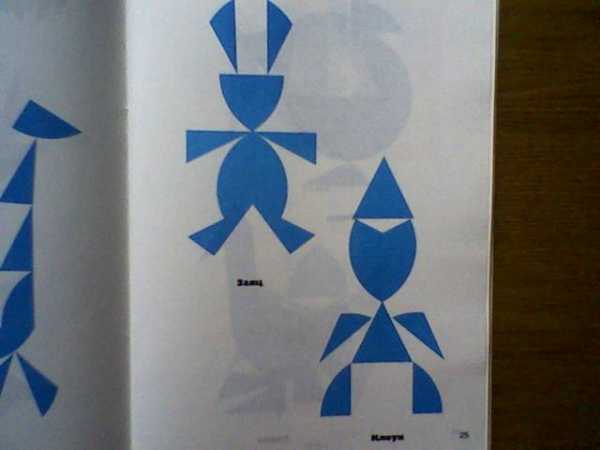
Пентамино

Известная логическая игра-головоломка. Именно эта игра вдохновила Алексея Пажитнова на создание популярной компьютерной игры тетриса.

Пентамино - очень популярная логическая игра и головоломка одновременно. Элементы в игре - плоские фигуры, каждая из которых состоит из пяти одинаковых квадратов. Всего существуют 12 элементов пентамино, обозначаемых латинскими буквами, форму которых они напоминают

Можно изготовить пентамино из кубиков, но тогда Вам нужно будет склеить и обклеить цветной пленкой 60 кубиков - трудновато. Предлагаем сделать элементы их плотного картона.

Рисуем каждый элемент на твердом картоне, вырезаем, проверяем, чтобы элемент входил в элемент “U”. Подрезаем , если надо лишнее. Мы рисовали детали из квадратиков 2,5х2,5 см.

Обводим готовый картонный элемент на сложенной вдвое цветной бумаге и вырезаем сразу две цветные детали. Лучше цветные детали делать меньше, чем картонные, и приклеиваются лучше, и углы поровнее будут.

Клеим клеем-карандашом цветную бумагу с двух сторон картонки.

Находим коробочку для хранения деталей, куда потом будем складывать также схемы и задания к игре.

Сложи прямоугольник.

Самая распространённая задача о пентамино — сложить из всех фигурок, без перекрытий и зазоров, прямоугольник. Поскольку каждая из 12 фигур включает в себя 5 квадратов, то прямоугольник должен быть площадью 60 единичных квадратов. Возможны прямоугольники 6×10, 5×12, 4×15 и 3×20.Существует ровно 2339 различных укладок пентамино в прямоугольник 6×10, а вот вариантов прямоугольника 3х20 всего 2.

Один из двух способов складывания прямоугольника 3х20

Честно скажу, пыталась весь вечер сложить - не получилось, поэтому ребенку такую задачу лучше не предлагать.

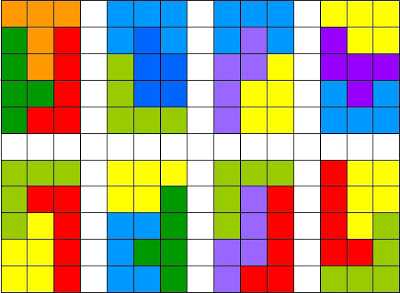
Детям лучше тренироваться на маленьких прямоугольниках из нескольких деталей.Вот нарисовали варианты складывания прямоугольников из трех деталей.

Сложи фигуру

Их элементов можно складывать различные фигуры, симметричные узоры, буква алфавита, цифры.Для маленьких детей, лучше фигуры складывать по образцу, как мозаику.Фигурки можно распечатать или перерисовать на листочек в клеточку

Ответы

ГЕКСАМИНО

Гексамино — это развивающая геометрическая головоломка-мозаика. На поле головоломки из отдельных деталей собрана причудливая геометрическая фигура. Все детали отличаются друг от друга по форме. Головоломка имеет четвертый уровень сложности и предназначена для детей в возрасте от 6 лет.

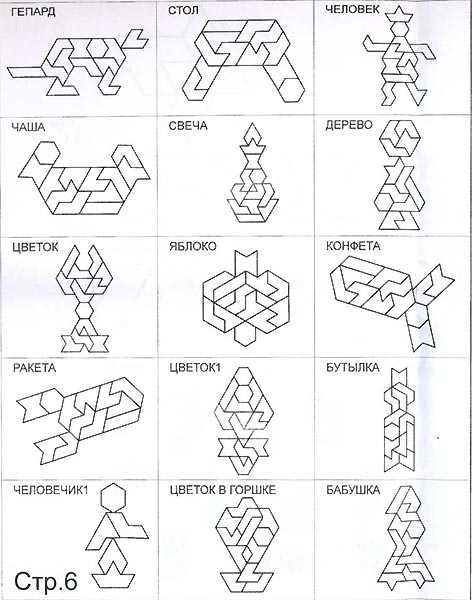
ГЕКСАТРИОН

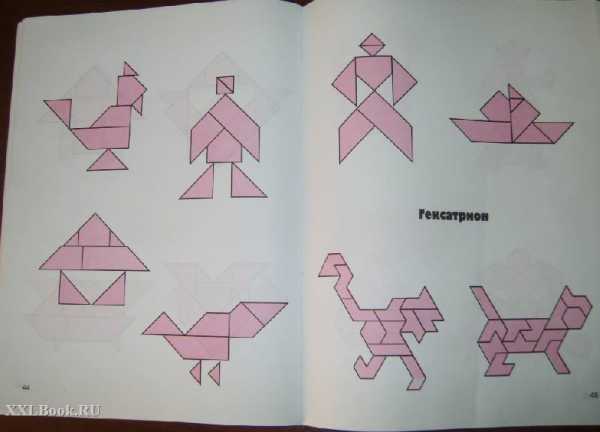ТЕТРИС

Классический Тетрис - случайные фигурки падают сверху, в игре игрок может переворачивать фигурки, двигать их горизонтально и ускорять движение вниз. Фигурка двигается пока не соприкоснется с другой фигуркой или не упадет на самый низ.

Если в игре заполняется ряд, то ряд исчезает и все что выше этого ряда опускается на одну клетку вниз. Игра постепенно наращивает темп. Если одновременно фигурки заполняют 4 ряда - это Тетрис, от этого и происходит название игры. В игре игрок получает очки за каждую фигурку и за каждый исчезнувший ряд. Игра Тетрис заканчивается когда верхняя фигурка касается верхней границы экрана.

Одна из самых классических игр, игра Тетрис (Tetris) обладает воистину магической притязательностью, сколько в неё не играешь, а хочется всё больше и больше. В игру Тетрис (Tetris) смогут играть не только взрослые, но и маленькие исследователи этого загадочного мира, игра тетрис всегда выручит и взбодрит скучными зимними вечерами. Итак, правила в игре такие же классические как и сама игра, складываем фигурки, так чтобы получилась одна сплошная линия. Тетрис - это одна из первых электронных игр, которая появилась еще тогда, когда ни у кого не было домашних компьютеров. Это самая современная и красочная версия тетриса. Дизайн и управление тут на высоте, кроме того добавлены некоторые интересные фишки. Цель игры - расставить падающие сверху фигурки таким образом, чтобы они заняли всё пространство по горизонтали, в этом случае они испарятся и дадут вам игровые очки.

novijmir.blogspot.com

Танграм — геометрическая головоломка

29 октября, 2012

Комментариев нет »

Игра служит для тренировки внимания, восприятия цвета, формы; способствует развитию у детей наглядно-образного мышления, воображения, комбинаторных способностей.

Танграм (кит.«семь дощечек мастерства») — древняя китайская головоломка, состоящая из семи плоских геометрических фигур, которые выкладывают в определенном порядке с целью получить различные более сложные фигуры в виде человека, животного, предмета домашнего обихода и т. д. Фигура, которую необходимо сложить, задаётся в виде силуэта или внешнего контура (в заданиях для взрослых и детей старше 7-ми лет) или в цвете с разложением на простые фигуры (для маленьких детей до 7-ми лет). При решении любого задания головоломки необходимо соблюдать два основных правила:

1- использовать все семь фигур танграма

2- фигуры не должны перекрываться между собой

Этот танграм изготовлен в домашних условиях из куска дощечки размером 15 x 15 см, толщиной 1 см путем распила на кусочки, шлифовки и окраски акриловыми красками.

Распиливаем большой квадрат, стороны которого равными 15 см, на части:2 маленьких прямоугольных треугольника (с гипотенузой, равной 15/2=7.5 см катетами 15/2√2≈5.3 см ),1 средний прямоугольный треугольник (гипотенуза 15/√2≈10.6 см и катеты 15/2=7.5 см),2 больших прямоугольных треугольника (гипотенуза 15 см и катеты 15/√2≈10.6 см),1 квадрат (со стороной 15/2√2≈5.3 см ),1 параллелограмм (со сторонами 15/2=7.5 см и 15/2√2≈5.3 см и углами 45° и 135º).

Прилагаются задания для детей до 7-ми лет:

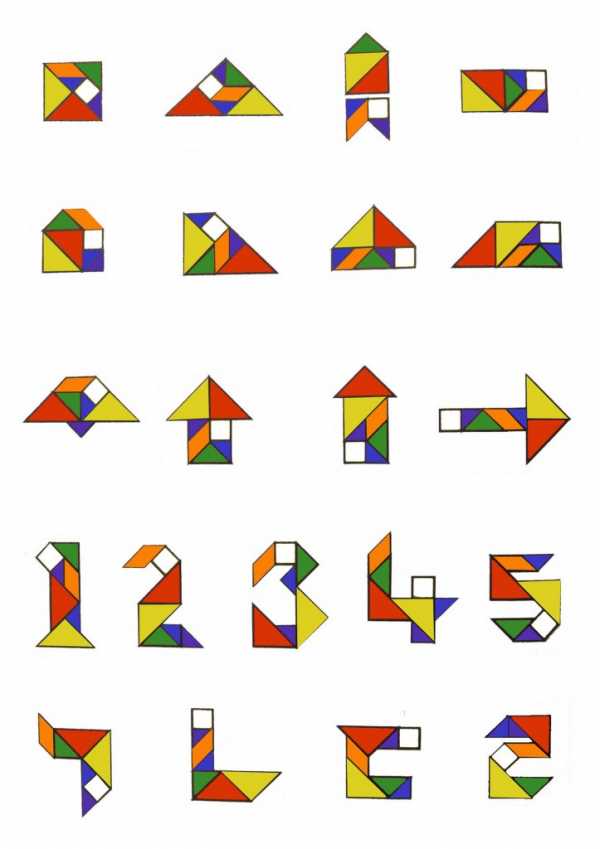
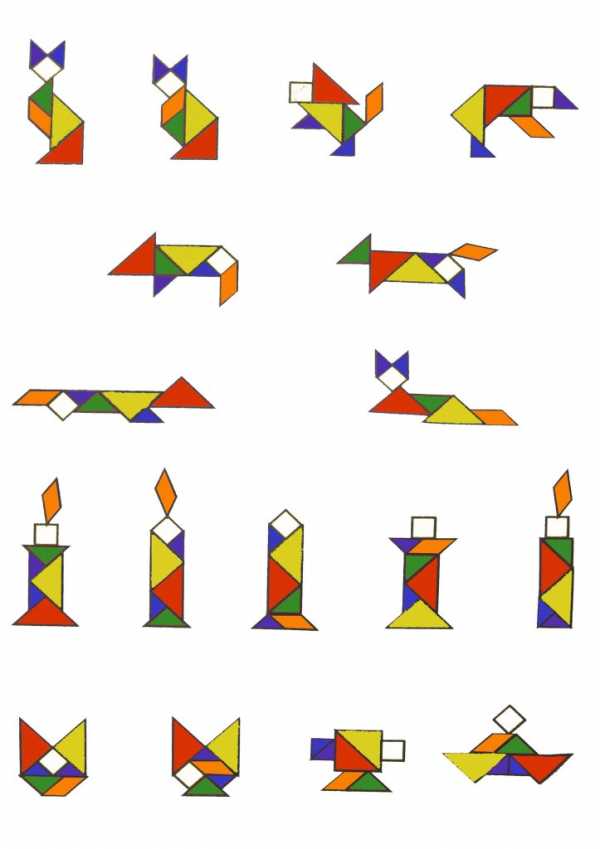
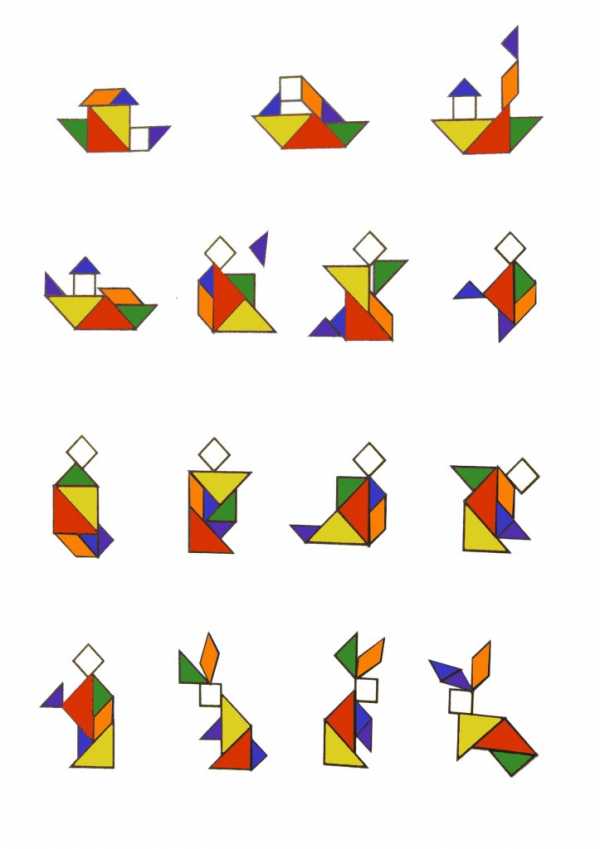
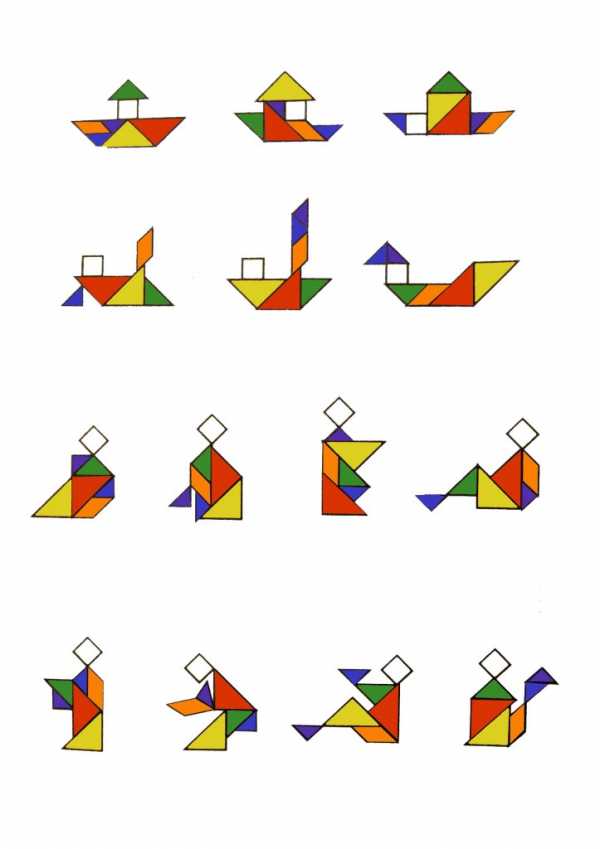
Задания для взрослых и детей старше 7-ми лет:

Комментариев нет.

mirdetey.by

Геометрические головоломки танграм, колумбово яйцо

Геометрические головоломки: танграм и колумбово яйцо

Геометрические головоломки развивают фантазию ребенка, пространственное представление. Во время игры ребенок учится составлять новые фигуры, вначале создают фигуры по образцу, затем по устному заданию в дальнейшем самостоятельно.

К геометрическим головоломка относятся:

Танграм
Колумбово яйцо

Эти головоломки не сложно сделать своими руками. Для этого вам потребуется плотный картон или пластик (возьмите старую пластиковую папку) или плотный фетр (фигурки из фетра понравятся маленьким детям). Начертите образец, вырезать лучше канцелярским ножом, игра готова.

Тангарм схема

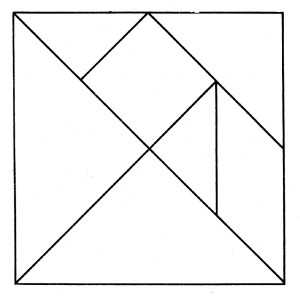В основе лежит квадрат 10х10 см (или другие размеры), он делится на 7 фигур, как на образце.

Танграм схемы распечатать

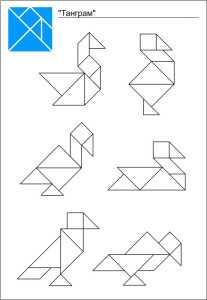
птица верблюд заяц

Колумбово яйцо

Чтобы изготовить игру Колумбово яйцо берем за основу овал (например 15 на 12 см), разрезаем как на рисунке. Получаем 10 частей.

А можно поступить по другому — в основе яйцо. Для этого рисуем окружность, проводим в ней 2 перпендикулярных диаметра — это первые линии, по которым в дальнейшем разрежем яйцо. Затем в крайних точках одного отрезка проводим 2 окружности, радиус каждой окружности равен диаметру первой окружности. Дальше, проводим линии, соединяющие три точки первой окружности, чтобы получить большой треугольник (на рисунке красные линии), заканчиваются линии на границе с большими окружностями.

Затем чертим еще 3 окружности с одинаковым радиусом.

1 окружность центр — вершина треугольника, радиус — отрезок от вершины треугольника до линии пересечения с большой окружностью.

2 окружность центр — точка пересечения диаметра с окружностью (внизу).

3 окружность центр — точка пересечения 2 окружности с диаметром.

1 окружность установила границы яйца, а 2 и 3 окружности дают точки для построения маленького треугольника. На рисунке линии красного цвета.

Обводим то что нам надо вырезать (на рисунке красный цвет)

само яйцо
вверху удлиняем линию диаметра до границы яйца
линии вверху яйца — линии через точки диаметра до пересечения с большой окружностью
внизу строим маленький треугольник, через точки пересечения окружности 2 и 3 с диаметром первой окружности.

Сверяемся с рисунком, получилось 10 частей головоломки. Вырезаем и играем.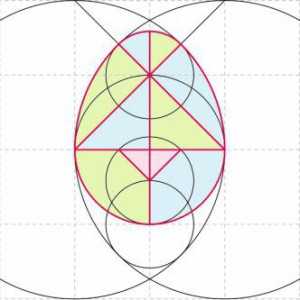

Колумбово яйцо схемы распечатать

razvitiedetei.info

Презентация по теме "Геометрические головоломки"

Государственное образовательное учреждение Тульской области «Тульская специальная (коррекционная) общеобразовательная школа-интернат для обучающихся, воспитанников с ограниченными возможностями здоровья»

Центр дистанционного образования

Презентация по теме

Геометрические головоломки

Игры на воссоздание из геометрических фигур образных и сюжетных изображений.

Автор – Юнг Е.А., учитель начальных классов, ЦДО

2014

Головоломки – игрушки на все времена. До появления компьютерных и бурного развития настольных игр, одним из основных развлечений для большинства людей была игра - головоломка "Танграм". В наше время очень много людей увлекаются головоломками. Они любимы не только детьми, но и взрослыми. Игра помогает развивать логическое мышление, геометрическую интуицию. Это способ отвлечения от повседневных проблем и направлен на развитие различных мыслительных процессов - сопоставление, обобщение, установление последовательности, определение отношений «целое» - «часть». Все эти умения необходимы будущим математикам.
Сейчас головоломки продают в разных исполнениях – и деревянные, и бумажные, и пластиковые.
На плоскости необходимо выкладывать любые фигуры, какие придумаешь или можно использовать образец. При этом нельзя накладывать части, чтобы они перекрывали друг друга. А также необходимо использовать все детали.

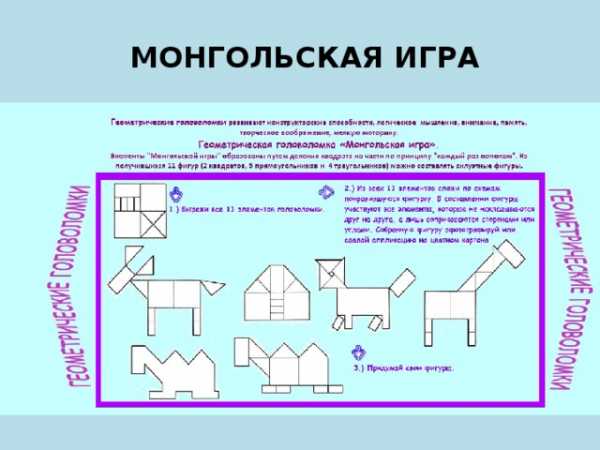
МОНГОЛЬСКАЯ ИГРА

ИГРА «ТАНГРАМ»

Танграм ( кит. 七巧板 , пиньинь qī qiǎo bǎn, букв. «семь дощечек мастерства») — головоломка , состоящая из семи плоских фигур , которые складывают определённым образом для получения другой, более сложной, фигуры (изображающей человека, животное, предмет домашнего обихода, букву или цифру и т. д.). Фигура, которую необходимо получить, при этом обычно задаётся в виде силуэта или внешнего контура. При решении головоломки требуется соблюдать два условия: первое — необходимо использовать все семь фигур танграма, и второе — фигуры не должны накладываться друг на друга.

Сколько больших треугольников?

Сколько маленьких треугольников?

Сколько средних треугольников?

Сколько всего треугольников и какого они размера?

Два больших два маленьких и один средний

Правила игры:

 В каждую собранную фигуру должны входить все семь элементов.
 При составлении фигур элементы не должны налегать друг на друга.
 Элементы фигур должны примыкать один к другому.
 Начинать нужно с того, чтобы найти место самого большого треугольника.
В результате игры получается плоскостное силуэтное изображение. Оно условно, схематично, но образ легко угадывается по основным характерным признакам предмета: его строению, пропорциональному соотношению частей и форме.

Танграм - очень древняя игра – головоломка. Она появилась в Китае более
4000 лет назад. Существует целый ряд версий и гипотез возникновения игры “Танграм”.
Легенда первая.

Разбитая плитка.

Более 4000 тысяч лет назад у одного человека из рук выпала фарфоровая плитка и разбилась на семь частей. Расстроенный, он в спешке старался ее сложить, но каждый раз получал все новые интересные изображения. Это занятие оказалось настолько увлекательным, что впоследствии квадрат, составленный из семи геометрических фигур, назвали Доской Мудрости.

Ши-Чао-Тю

Легенда вторая: три мудреца придумали «Ши-Чао-Тю».

Появление этой китайской головоломки связано с красивой легендой.

Почти две с половиной тысячи лет тому назад у немолодого императора Китая родился долгожданный сын и наследник. Шли годы. Мальчик рос здоровым и сообразительным не по летам. Одно беспокоило старого императора: его сын, будущий властелин огромной страны, не хотел учиться. Мальчику доставляло большее удовольствие целый день забавляться игрушками. Император призвал к себе трех мудрецов, один из которых был известен как математик, другой прославился как художник, а третий был знаменитым философом, и повелел им придумать игру, забавляясь которой, его сын постиг бы начала математики, научился смотреть на окружающий мир пристальными глазами художника, стал бы терпеливым, как истинный философ, и понял бы, что зачастую сложные вещи состоят из простых вещей. Три мудреца придумали "Ши-Чао-Тю"- квадрат, разрезанный на семь частей.

Семь книг Тана

Легенда третья: семь книг Тана.

«В записках покойного профессора Челленора, попавших в руки автора, — утверждал Лойд, — имеются сведения о том, что семь книг о танграмах, каждая из которых насчитывает ровно тысячу фигур, были составлены в Китае более 4000 лет назад. Эти книги ныне стали столь большой редкостью, что за те сорок лет, которые профессор Челленор провел в Китае, ему лишь раз удалось видеть первое издание первого из семи томов».

Согласно легенде Лойда, Тан был легендарным китайским мудрецом, которому его соотечественники поклонялись как божеству. Фигуры в своих семи книгах он расположил в соответствии с семью стадиями в эволюции Земли. Его танграмы начинаются с символических изображений хаоса и принципа «инь и ян». Затем следуют простейшие формы жизни, по мере продвижения по древу эволюции появляются фигуры рыб, птиц, животных и человека. По пути в различных местах попадаются изображения того, что создано человеком: орудия труда, мебель, одежда и архитектурные сооружения. Лойд часто цитирует высказывания Конфуция, философа по имени Шуфуце, комментатора Ли Хуанчжан и вымышленного профессора Челленора. Ли Хуанчжан упоминается в связи с тем, что по преданию он знал все фигуры из семи книг Тана прежде, чем научился говорить. Встречаются у Лойда и ссылки на «известные» китайские пословицы типа «Только глупец взялся бы написать восьмую книгу Тана».

Первое изображение танграма (1780) обнаружено на ксилографии японского художника Утомаро, где две девушки складывают фигурки. Название "танграм" возникло в Европе, вероятнее всего, от слова "тань" (что означает "китаец") и корня "грамма" (в переводе с греческого "буква") На первых порах им пользовались не для развлечения, а для обучения геометрии.

http ://festival.1september.ru/articles/626772/

Танграм, возможно, ведёт своё происхождение от названия вида мебели, появившегося во времена империи Сун ., а в дальнейшем слово превратилась в набор деревянных фигурок для игры.
Писатель и математик Льюис Кэрролл считается энтузиастом танграма. У него хранилась китайская книга с 323 задачами.
У Наполеона во время его изгнания на остров Святой Елены был набор для танграма и книга, содержащая задачи и решения.
Книга Сэма Лойда «Восьмая книга Тан» ( англ. The Eighth Book Of Tan ), вышедшая в 1903 году , содержит вымышленную историю танграма, согласно которой эта головоломка была изобретена 4 тысячи лет назад божеством по имени Тан. Книга включает 700 задач, некоторые из которых неразрешимы.

Какую фигуру составили?

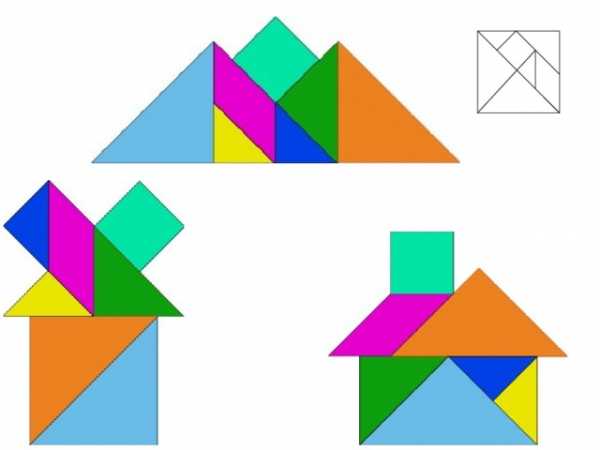
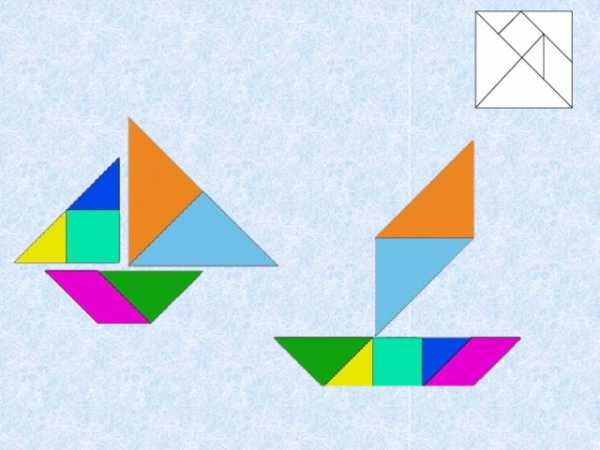
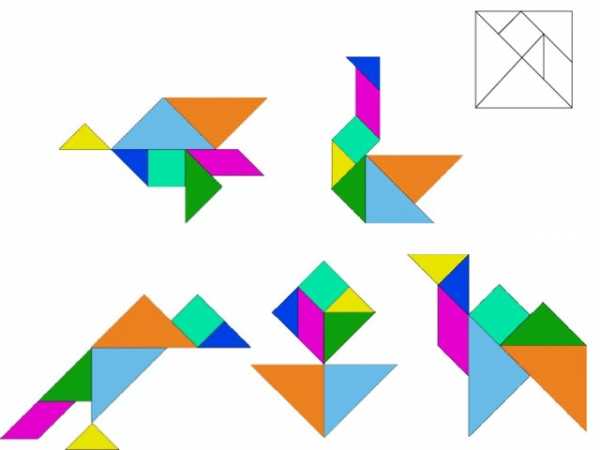
"Очарование танграма состоит в простоте материала и в кажущейся его непригодности для создания фигурок, обладающих эстетической привлекательностью»

М. Гарднер:

ИГРА “КОЛУМБОВО ЯЙЦО”

Колумбово яйцо — крылатое выражение, обозначающее неожиданно простой выход из затруднительного положения.
Жил-был в 16 веке итальянец Джироламо Бенцони. Он любил путешествовать. И однажды на обеде у кардинала Мендосы он встретил Колумба. Там и произошла эта история.По преданию, когда Колумб во время обеда у кардинала Мендосы рассказывал о том, как он открывал Америку, веке итальянец Джироламо Бенцони сказал: «Что может быть проще, чем открыть новую землю?» В ответ на это Колумб предложил ему простую задачу: как поставить яйцо на стол вертикально? Когда ни один из присутствующих не смог этого сделать, Колумб, взяв яйцо, разбил его с одного конца и поставил на стол, показав, что это действительно было просто. Увидев это, все запротестовали, сказав, что так смогли бы и они. На что Колумб ответил: «Разница в том, господа, что вы могли бы это сделать, а я сделал это на самом деле».

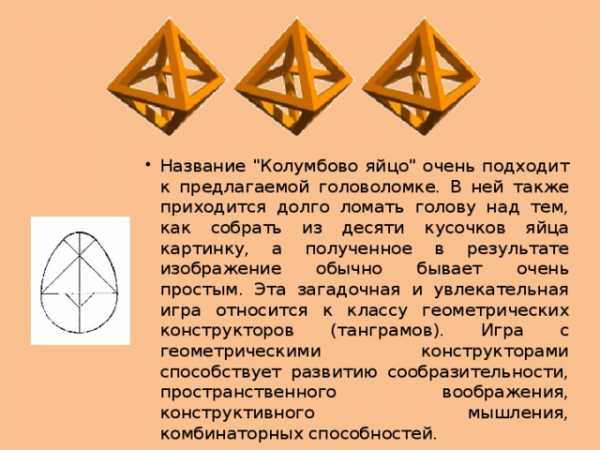
Название "Колумбово яйцо" очень подходит к предлагаемой головоломке. В ней также приходится долго ломать голову над тем, как собрать из десяти кусочков яйца картинку, а полученное в результате изображение обычно бывает очень простым. Эта загадочная и увлекательная игра относится к классу геометрических конструкторов (танграмов). Игра с геометрическими конструкторами способствует развитию сообразительности, пространственного воображения, конструктивного мышления, комбинаторных способностей.

ИГРА “КОЛУМБОВО ЯЙЦО” - это овал из 10 частей: среди них 4 треугольника( 2 больших и 2 маленьких), 2 фигуры, похожие на четырехугольник, одна из сторон которой округлой формы, 4 фигуры( большие и маленькие),имеющие сходство с треугольником, но с закругленной одной стороной.

. Лучше всего из деталей головоломки "Колумбово яйцо" составлять силуэты птиц (известно 54 различных форм птиц), можно также составить силуэты предметов, людей, животных.

Какую фигуру составили?

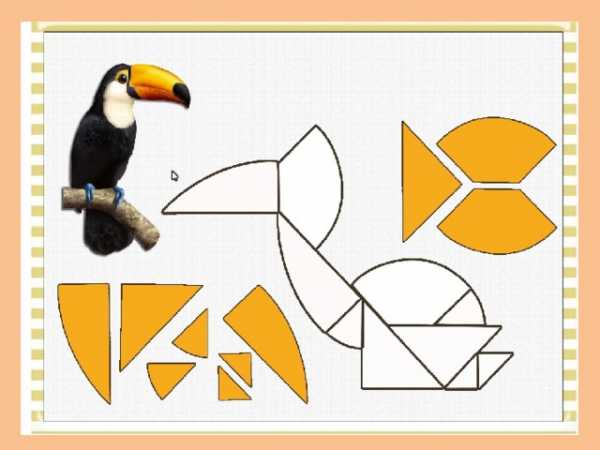
Геометрические головоломки – замечательное средство для развития ума, ещё и головоломки можно использовать для создания интерьера:
http://www.lobzik.pri.ee/modules/news/article.php?storyid=645

Мебельная головоломка

Куб

http://www.youtube.com/watch?v=JClq8XIuK6M

Куби-Гами ( Cubigami)

http://yandex.ru/video/search?p=1&filmId=nMtgVgv_UXI&text=%D0%B3%D0%B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B5%20%D0%B3%D0%BE%D0%BB%D0%BE%D0%B2%D0%BE%D0%BB%D0%BE%D0%BC%D0%BA%D0%B8&_=1417688865574&safety=1

Головоломка - развивающая игра для любого возраста, направленная на усиление пространственного восприятия и воображения.

Головоломки развивают умственные и творческие способности, пространственное воображение, комбинаторные способности, логическое мышление, сообразительность, смекалку, а также усидчивость и мелкую моторику, формирует внимательность, упорство в достижении цели, способствует творческому поиску чего – то нового, учится терпению и последовательности.

Что интересного было на занятии?
Что особенно запомнилось?
Какой композиции вы бы отдали предпочтение? Почему?

Источники:

http ://www.golovolomok.net/component /

http://yandex.ru/video/search?p=1&filmId=nMtgVgv_UXI&text=%D0%B3%D0%B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B5%20%D0%B3%D0%BE%D0%BB%D0%BE%D0%B2%D0%BE%D0%BB%D0%BE%D0%BC%D0%BA%D0%B8&_= 1417688865574&safety=1
http:// www.youtube.com/watch?v=JClq8XIuK6M
http:// www.lobzik.pri.ee/modules/news/article.php?storyid=645
http://festival.1september.ru/articles/626772 /
Анимация:
http://yandex.ru/images/search?img_url=http%3A%2F%2Fwww.mathpuzzle.com%2FInterlockingSpiralsAnimation.gif&uinfo=sw-1525-sh-858-ww-1506-wh-708-pd-0.89552241563797-wp-16x9_1366x768&_=1417717151222&p=2&viewport=wide&text=%D0%B3%D0%B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B5%20%D1%84%D0%B8%D0%B3%D1%83%D1%80%D1%8B%20%D0%B0%D0%BD%D0%B8%D0%BC%D0%B0%D1%86%D0%B8%D1%8F&pos=60&rpt=simage&pin=1
http:// myweb.rollins.edu/jsiry/Deep_technology_tetrahedron.html
http:// animating.ru/avatars/category_25.htm

kopilkaurokov.ru

Танграм

Танграм (кит. 七巧板, англ. Tangram) — головоломка, которая состоит из семи плоских частей – геометрических фигур (двух больших треугольников, одного среднего треугольника, двух маленьких треугольников, одного квадрата и одного параллелограмма).

Цель головоломки состоит в том, чтобы сложить из всех семи частей заданные фигуры. Это могут быть изображения людей, животных, предметов домашнего обихода, букв, цифр и т. д. Фигура, которую необходимо получить, при этом обычно задаётся в виде силуэта или внешнего контура. При решении головоломки требуется соблюдать два условия: первое — необходимо использовать все семь фигур танграма, и второе — фигуры не должны накладываться друг на друга.

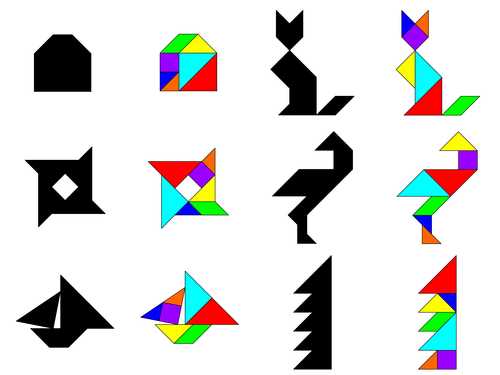
Книга Рональда Рида «Танграм: 330 задач» (англ. Tangrams: 330 Puzzles) просит читателей присылать любые другие фигуры. Такое условие создаёт множество хотя и с гораздо большим числом элементов, чем множество выпуклых фигур, но всё же конечное. В ответ было предложено приблизительно 6,13 миллиона возможных конфигураций, в каждой из которых при этом хотя бы одна вершина и хотя бы одна сторона любой части совпадают с вершиной и стороной другой части.

Многие китайские ученые считают, что корни танграма восходят к династии Сун (960-1127), когда Хуан Боси (1079-1118) изобрел набор прямоугольных столов и схемы их расстановки на банкете.

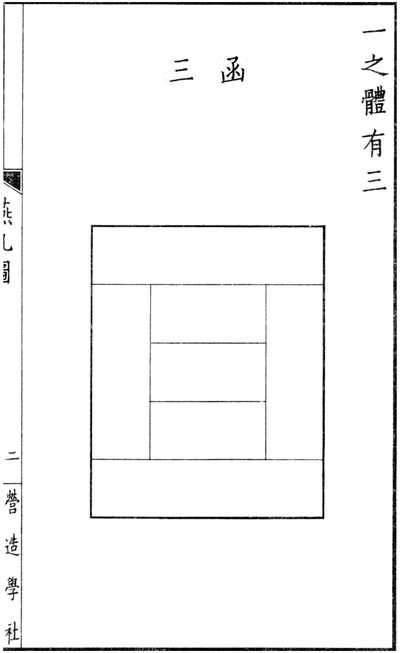
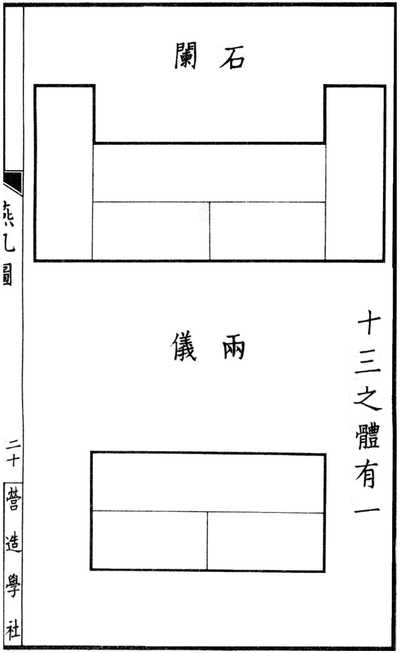
Во время династии Мин (1368-1644) в 1617 году Джи Шан описал расположение на банкете столов треугольной формы. Со временем, в середине династии Цин (1644-1911) столы на банкетах имели форму известных нам ныне семи частей танграма.

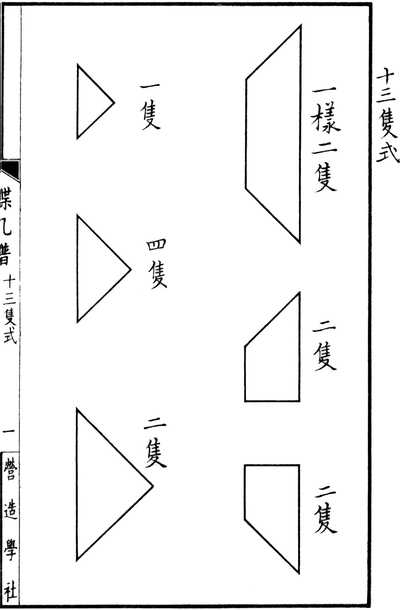
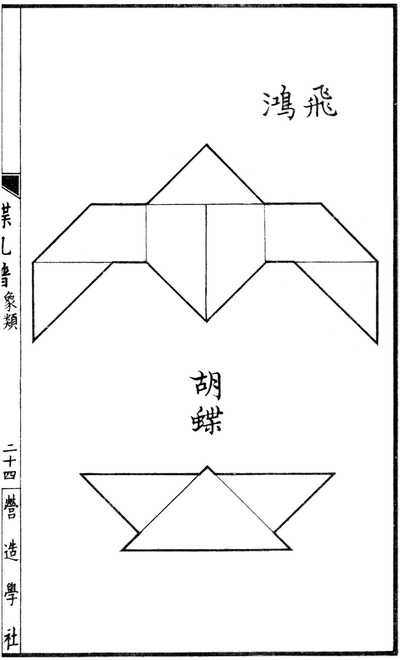
Столы-танграм в Льюань, Сучжоу

В это же время появляется и головоломка «Танграм». Она пользовались большой популярностью во всех социальных слоях населения, в том числе и у императорской семьи. Головоломку начали производить и для продажи иностранным купцам. Старейший такой экземпляр, был куплен в Кантоне Робертом Валном (Robert Waln) в 1802 году. Головоломка сделана из слоновой кости. Она хранится в Ryerss Museum в Калифорнии.

Хотя головоломка в Америке и Европе известна с 1802, самые ранние силуэты для сборки были опубликованы в 1813 в книге Би Ву Юши и Санг Ся Кэ (Bi Wu Jushi and Sang Xia Ke) «Сборник диаграмм танграма» (Compilation of Tangram Diagrams). В период с 1817 по 1818 год, книги о танграме были опубликованы в Англии, Франции, Швейцарии, Италии, Нидерландах, Дании, Германии и США.

Несмотря на всю кажущуюся простоту, этой головоломкой интересовались мэтры занимательной математики – Генри Дьюдени, Сэм Лойд, Льюис Кэрол.

Книга Сэма Лойда «Восьмая книга Тан» (англ. The Eighth Book Of Tan), вышедшая в 1903 году, содержит вымышленную историю танграма, согласно которой эта головоломка была изобретена 4 тысячи лет назад божеством по имени Тан. Книга включает 700 задач, некоторые из которых неразрешимы.

Есть у танграма и свои парадоксы. Парадокс танграма заключается в следующем: каждый раз полностью используя весь набор, можно сложить две фигуры, одна из которых будет подмножеством другой. Один такой случай приписывается Генри Дьюдени: две похожие фигуры изображают монахов, но у одной из них при этом есть нога, а у другой фигуры её нет. Некоторые из этих парадоксов представлены ниже.

Существуют и трёхмерные магнитные версии танграма:

Танграм продолжает быть популярным и в наши дни. Ему находится применение в различных областях.

В дизайне мебели:

В дизайне одежды, украшений, сумок:

В кулинарии:

Шоколадный танграм

Форма для выпечки

Посуда

В живописи:

В быту:

Дверная ручка

Шкатулка

Чехол для iPhone

И конечно же головоломка "Танграм" остаётся предметом искусства:

puzzlepedia.ru

"Колумбово яйцо" — увлекательная головоломка для детей и взрослых

Игры, которые заставляют думать, всегда будут популярными, каким бы технологичным ни был век. Головоломки развивают логическое мышление. А если они используют наглядный материал, то еще и образное. Игры на основе различных по форме и размеру геометрических фигур помогают развить пространственное воображение. Танграм, в частности "Колумбово яйцо", формирует такие мыслительные процессы, как сопоставление части и целого, анализ ситуации и обобщение.

Какими бывают головоломки?

Любое задание, для решения которого потребуется проявить сообразительность, будет относиться к головоломкам. В нем для поиска ответа не нужны специальные научные знания. Здесь, скорее, потребуются интуиция и творчество.

Особой классификации головоломок нет. Однако можно разделить их на группы в зависимости от того, чем они оперируют.

Основа игры — слово. Само задание, ход его решения и результат — все можно выполнить только с использованием устной или письменной речи. Эта головоломка не требует привлечения предметов. Ее примером может служить загадка или шарада.
Задание с использованием предметов. Оно может быть сложено из любых вещей, которые обязательно найдутся в доме: спичек или зубочисток, монет или пуговиц, карт.
Головоломка, изображенная на бумаге. Сюда относятся все виды кроссвордов и ребусы.
Игры со специально изготовленными предметами. Популярные примеры: пазлы, кубик Рубика, змейка, "Колумбово яйцо".

Что такое геометрическая головоломка?

Для этой игры основная фигура делится на части. Получаются плоские, правильные и не очень детали. Изначальная фигура может быть практически любой. В танграме, например, это обычно квадрат. А из названия головоломки «Колумбово яйцо» ясно, что в основе лежит овал, который напоминает яйцо. Встречаются игры, в которых главной фигурой является круг или сердечко.

Из получившихся деталей нужно сложить что-то другое, какую-то сложную фигуру. И этот рисунок должен быть узнаваем. Такое складывание может быть как произвольным, так и по заданию. Схемы для составления рисунков могут содержать только силуэты или изображать контуры деталей. Все зависит от уровня подготовки игрока.

Как сделать головоломку самому?

Как и любую другую игрушку, такие конструкторы можно приобрести в магазине. Но интереснее будет, если сделать "Колумбово яйцо" своими руками.

Поскольку предполагается многократное использование деталей конструктора, то желательно, чтобы материал был плотным. Например, твердый картон или кусок ровного пластика.

Для того чтобы упростить процесс изготовления игры, можно взять за основу овал, который разлиновать так же, как и яйцо. Но можно потратить немного больше времени и начертить яйцо.

Для начала нужно нарисовать окружность, в которой провести два перпендикулярных диаметра. Они станут первыми линиями, по которым потом будет разрезаться яйцо. Потом в крайних точках одного из отрезков провести две окружности с радиусом, равным этому диаметру. Затем нужно прочертить линии, соединяющие три точки на окружности, которые дадут большие треугольники. Закончить их нужно на больших окружностях. Начертить верхнюю маленькую окружность и нижнюю такого же радиуса. Первая покажет границу яйца, а нижняя даст три точки, которые подскажут, где начертить маленькие треугольники.

В итоге должно получиться 5 пар фигур, которые образованы:

из больших и маленьких треугольников;
больших и маленьких фигур, напоминающих треугольники, но с одной закругленной стороной;
деталей, напоминающих трапецию, одна сторона которой выгнута.

Для наглядности и более легкого понимания того, как разлиновать "Колумбово яйцо", схема представлена ниже. Линии, по которым нужно разделить головоломку на части, выделены красным цветом.

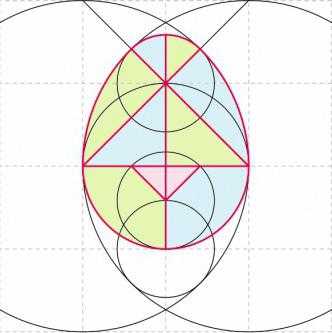
В некоторых вариантах этой игры для упрощения задания маленькие треугольники внутри яйца объединяются в один.

Правила игры с головоломкой

Суть задания состоит в том, чтобы из деталей конструктора «Колумбово яйцо» сложить фигурки. Это могут быть люди, животные или птицы, транспорт и мебель, цветы, буквы и цифры.

В игре существует только два правила, которые нельзя нарушать:

первое - нужно использовать все детали;
второе - части не должны пересекаться, их следует прикладывать друг к другу.

При знакомстве с головоломкой можно просто рассмотреть детали и подумать о том, на что они похожи. Это упростит игру в "Колумбово яйцо". Для дошкольников данный пункт просто необходим. Потому что так им будет проще понять, как составить фигурки. К тому же этот момент способствует развитию воображения и умению анализировать и разбивать целое на части.

По мере совершенствования навыков игры с головоломкой нужно перемещаться от простого к сложному. Сначала схемы должны содержать линии, которые показывают границы деталей. Потом их может уже не быть.

Складывать фигурки желательно на белом листе бумаги. Потом их можно обвести и подрисовать уточняющие детали и фон. Это поможет развить воображение и разнообразить игру.

Возможные схемы головоломки

Как пример упрощенного варианта игры, в котором 9 частей, на начальном этапе можно использовать такие схемы.

Для знатоков и любителей поломать голову подойдут картинки без вспомогательных линий.

Никто не останется равнодушным. Вся семья будет задействована в поисках решения.

fb.ru

Исследовательская работа "Геометрические головоломки" - математика, прочее

Оглавление

1.Введение………………………………………………………………… 2 -3 стр.

2.Основная часть …...……..….................................................................. 4 – 10стр.

2.1. Виды геометрических головоломок…………………………4 стр.

2.2. История зарождения геометрических головоломок………. 4 - 6 стр.

2.3. Правила геометрических головоломок и изготовление…... 6 - 9 стр.

2.4. Применение геометрических головоломок в современном мире...................................................................................................... 9 стр.

3. Результаты анкетирования и эксперимента……................................ 10 -12 стр.

4. Выводы..................................................................................................... 13 стр.

5. Список использованной литературы и источников…........................ 14 стр.

6. Приложение …………………………………………………………. 15-17стр.

Введение

На уроках математики мы познакомились с геометрическими фигурами научились чертить их на линованной и нелинованной бумаге, вырезать из картона и составлять из них новые фигуры в виде предметов быта, животных, растений. Это оказалось очень увлекательным занятием. Учитель математики сказала, что фигуры используются ещё и в геометрических головоломках: «Танграм», «Колумбово яйцо», «Полимино».Стало интересно узнать, что такое головоломка, где они появились и встречаются ли сейчас.

Не все учебники математики содержат задания направленные на решение геометрических головоломок. Внеурочная деятельность учащихся начального и среднего звеньев школытакже не предусматривает рассмотрение указанных задач. На практике можно убедиться, что молодое поколение даже не слышали о многих геометрических головоломках, хотя и понимают значимость их на развитие умственных способностей людей. Самое главное, что в олимпиадах и конкурсах по математике в последнее время включают задания с геометрическими головоломками. Всё это определяетактуальность данной исследовательской работы.

Несомненной является и новизнаданной работы, так какисследования по теме «Геометрические головоломки» в МКОУ «Брылинская СОШ» ранее не проводились и их изучение не предусмотрено школьной программой по математике.

Данное исследование может быть использовано учителем математики на уроках в виде дополнительных заданий для развития воображения, мышления, интереса к предмету. Также возможно применение нашего материала во внеурочной деятельности, например, учителями начальной школы или воспитателями в детском саду. Хотелось бы, чтобы геометрические головоломки стали альтернативой телефонным играм в организации досуга школьников (например, на переменах между уроками). Это говорит о высоком практическом значении исследования.

В ходе исследования использованы материалы следующих сайтов: «Мир детских эмоций и чувств» (https://ncuxolog.ru/zagadochnyj-tangram), «Детский сайт для родителей. Развитие детей» (http://razvitiedetei.info/dosug/geometricheskij-konstruktor-tangram.html), «Волшебная шкатулка. Занимательная математика» (http://novijmir.blogspot.ru/p/blog-page_17.html). С этих сайтов мы взяли материал о истории зарождения геометрических головоломок, правила игр и способы изготовления элементов геометрических головоломок.Проанализировали статью, представленную на web - страницах сайта«Ярмарка мастеров» (https://www.livemaster.ru/topic/463495-v-mire-tangram-igrushka-na-vse-vremena), в которой описывается применение геометрических головоломок в жизни людей. Прочитали работу Д.Головина, Е. Дубровского и др. в электронном журнале «Юный ученый». В словарях русского языка С.И. Ожигова и Т.В. Ефремова рассмотрели толкование некоторых слов по нашей теме.

Объект исследования:игры«Танграм», «Колумбово яйцо», «Полимино».

Предмет: знание геометрических головоломок и интерес людей к ним.

Цель исследования: выявление степени знания и увлеченности людьми геометрическими головоломками.

Задачи:

Определить виды головоломок.
Изучить историю появления геометрических головоломок.
Изучить правила игры.
Выявить применение геометрических головоломок в современном мире.
Провести опрос среди населения на знание и увлеченность геометрическими головоломками.
Провести эксперимент среди школьников.
Систематизировать полученные данные в диаграммах.

Гипотеза - предположим,чтоучащиеся и взрослые люди мало знают о геометрических головоломках и мало ими увлекаются.

Методы исследования:

Этапы работы:

определение темы;
определение цели и задач;
выдвижение гипотезы;
отбор информации из различных источников;
проведение анкетирования населения;
систематизация полученной информации ;
оформление работы;
презентация работы.

Сроки работы над исследованием: декабрь 2016 -март 2017 г.

Основная часть
1. Виды головоломок

По новому словарю русского языка Т.В. Ефремова - головоломка:

а) Специально подобранная загадка, задача и т.п., для решения которой требуются сообразительность и знания в соответствующей области.

б) Забавная поделка, состоящая из различных соединенных между собою элементов, которые необходимо разъединить.

2) перен. Какие-л. сложные проблемы, решение которых требует большого труда[2].

Виды головоломок:

Устные головоломки – это головоломки, условия которых может быть передано в устной речи без привлечения каких – либо дополнительных предметов. К ним можно отнести: загадки, шарады, парадоксы, игру данетки.
Головоломки с предметами – это головоломки, в которых активно используются обычные бытовые предметы: головоломки со спичками, монетами, карточные головоломки.
Механические головоломки – это класс головоломок, которые специально были изготовлены как головоломки. Это всевозможные проволочные головоломки, головоломки типа Кубика Рубика, пазлы, пентамино и др.
Печатные головоломки – это те головоломки, для которых необходима бумага и карандаш. Они могут быть напечатаны или нарисованы. К таким головоломкам относятся сконворды, кроссворды, ребусы и т.д.
Компьютерные головоломки.[5.7]

Среди множества головоломок имеет особое значение геометрические, т. е. такие, в которых применяются геометрические фигуры: «Танграм», «Колумбово яйцо», «Полимино».

История зарождения геометрических головоломок

«Танграм»

Игра родилась в Китае более 4000 лет назад. Хотя слово «Танграм» было придумано чуть более века назад в Северной Америке, китайская игра была известна под названием «доска из семи фигур мудрости»[5.2].

В учебнике Г.К. Муравина, О.В. Муравиной «Математика. 5класс.» говорится о том, что название «Танграм» возникло в Европе и, вероятнее всего, переводится как «китайские буквы», так как в переводе с греческого «тань» означает «китаец», а «грамм» - «буква». Рассказывают, что Наполеон, находясь в изгнании на острове Св. Елены, часами занимался составлением картинок из элементов «танграма»[3].

Существует множество легенд о зарождении игры. В нашей работе приводим три, самые занимательные и поучительные.

Легенда первая: версия про разбитую плитку.

Легенда вторая: три мудреца придумали «Ши-Чао-Тю».

Почти две с половиной тысячи лет тому назад у немолодого императора Китая родился долгожданный сын и наследник. Мальчик рос здоровым и сообразительным не по летам.Одно беспокоило старого императора: его сын, будущий властелин огромной страны, не хотел учиться. Мальчику доставляло большее удовольствие целый день забавляться игрушками. Император призвал к себе трех мудрецов, один из которых был известен как математик, другой прославился как художник, а третий был знаменитым философом, и повелел им придумать игру, забавляясь которой, его сын постиг бы начала математики, научился смотреть на окружающий мир пристальными глазами художника, стал бы терпеливым, как истинный философ, и понял бы, что зачастую сложные вещи состоят из простых вещей. Три мудреца придумали "Ши-Чао-Тю"- квадрат, разрезанный на семь частей[5.2].

Легенда третья: семь книг Тана.

Согласно легенде Лойда, Тан был легендарным китайским мудрецом, которому его соотечественники поклонялись как божеству. Фигуры в своих семи книгах он расположил в соответствии с семью стадиями в эволюции Земли. Его танграмы начинаются с символических изображений хаоса и принципа «инь и ян». Затем следуют простейшие формы жизни, по мере продвижения по древу эволюции появляются фигуры рыб, птиц, животных и человека. По пути в различных местах попадаются изображения того, что создано человеком: орудию труда, мебель, одежда и архитектурные сооружения. Лойд часто цитирует высказывания Конфуция, философа по имени Шуфуце, комментатора Ли Хуанчжан и вымышленного профессора Челленора. Ли Хуанчжан упоминается в связи с тем, что по преданию он знал все фигуры из семи книг Тана прежде, чем научился говорить. Встречаются у Лойда и ссылки на «известные» китайские пословицы типа «Только глупец взялся бы написать восьмую книгу Тана»[5.6].

Колумбово яйцо— крылатое выражение, обозначающее неожиданно простой выход из затруднительного положения[5.3] .

Существует красивый миф о происхождении этого выражения.

Открыватель Америки Колумб был приглашен к всемогущему кардиналу Мендозе. За столом, по просьбе гостей, он начал рассказывать, как именно был им открыт Новый Свет (который, впрочем, он считал Индией). Кто-то из присутствующих, человек ограниченный, но самоуверенный, пожав плечами, сказал: «Так просто всё?»Колумб взглянул на него и протянул ему лежавшее на блюде куриное яйцо: «Сделайте так, чтобы оно стояло на своем носке». Разумеется, попытки установить яйцо успехом не увенчались. «Это немыслимо...» - сказал обескураженный собеседник Колумба. «Это очень просто!» - с усмешкой ответил мореплаватель и, разбив о стол носок яйца, без труда заставил его стоять.

Выражение «колумбово яйцо» - стало воплощением остроумного и неожиданного выхода из затруднения, синонимом простого разрешения трудных вопросов.[5.4]А затем стало названием геометрической головоломки.Суть задания состоит в том, чтобы из деталей конструктора «Колумбово яйцо» сложить фигурки. Это могут быть люди, животные или птицы, транспорт и мебель, цветы, буквы и цифры.

«Полимино»

Полимино, или полиомино (англ. polyomino) — плоские геометрические фигуры, образованные путём соединения нескольких одноклеточных квадратов по их сторонам.

Полимино использовались в занимательной математике, по крайней мере с 1907 года, а известны были ещё в древности. Многие результаты с фигурами, содержащими от 1 до 6 квадратов, были впервые опубликованы в журнале «FairyChessReview» в период с 1937 по 1957 г., под названием «проблемы рассечения». Название «полимино» или «полиомино» было придумано Соломоном Голомбом в 1953 году и затем популяризировано Мартином Гарднером[1].

2.3. Правила головоломок и изготовлениеэлементов для игры

«Танграм»

В игре – головоломке «Танграм» главной целью является создание фигур из 7 элементов –танов, полученных разрезанием квадрата на семь частей – два больших (1, 2), два маленьких (3, 4) и один средний треугольник (5), один квадрат (6) и один параллелограмм (7)[5.6](рис.1). При решении головоломки требуется соблюдать условия: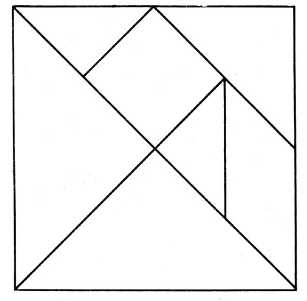

Рисунок 1. Основа игры "Танграм"

- при составлении изображений используются все семь фигур;

- фигуры должны быть в одной плоскости, т.е. не должны перекрывать друг друга, располагаться поверх других частей;

-все части должны быть смежными, т.е. иметь точку соприкосновения с другими частями[5.2].

На курсе «Математика в задачах» учащиеся 6 класса познакомились с «Танграм» и попробовали составить свои фигуры (Приложение №1).

«Колумбово яйцо»

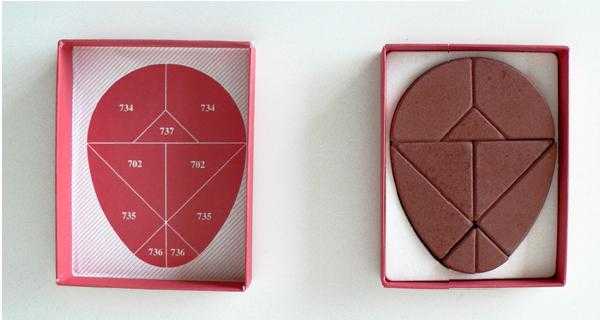
В головоломке «Колумбово яйцо» так же, как и в «Танграм», необходимо создавать фигуры из элементов, которые получают из овала. В игре существует только два правила, которые нельзя нарушать: первое - нужно использовать все детали- 10штук; второе - части не должны пересекаться, их следует прикладывать друг к другу(рис. 2).

Для изготовления игры берут за основу овал (например 15 на 12 см), разрезают, как на рисунке 2. Получают 10 частей.А можно поступить по - другому — в основе яйцо. В окружности проводим 2 взаимно перпендикулярных диаметра — это первые линии, по которым в дальнейшем разрезаем яйцо. Затем в крайних точках одного отрезка проводим 2 окружности, радиус каждой окружности равен диаметру первой окружности. Дальше, проводим линии, соединяющие три точки первой окружности, чтобы получить большой треугольник (на рисунке красные линии), заканчиваются линии на границе с большими окружностями.Затем чертим еще 3 окружности с одинаковым радиусом: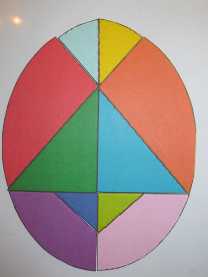

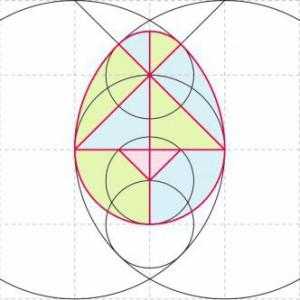
Рисунок 2. Основа игры "Колумбово яйцо"

1 окружность: центр — вершина треугольника, радиус — отрезок от вершины треугольника до линии пересечения с большой окружностью.

2 окружность: центр — точка пересечения диаметра с окружностью (внизу).

3 окружность: центр — точка пересечения 2 окружности с диаметром.

Обводим то что нам надо вырезать (на рисунке красный цвет)

само яйцо
вверху удлиняем линию диаметра до границы яйца
линии вверху яйца — линии через точки диаметра до пересечения с большой окружностью

внизу строим маленький треугольник, через точки пересечения окружности 2 и 3 с диаметром первой окружности.Сверяемся с рисунком, получилось 10 частей головоломки. Вырезаем и играем[5.5]. Из них можно составить множество интересных фигур - животных, птиц и т.д., лишь бы был интерес и воображение.

Рисунок 3. Фигуры из элементов "Колумбово яйцо"

«Полимино»

Головоломку «Полимино» можно подразделить на виды, в зависимости от количества квадратиков (рис.3). Из квадратов, соседствующих сторонами, можно сложить n-ое количество различных простых фигур (рис.2), а из них более сложные геометрические фигуры.

Рисунок 4. Виды полимино.

Все названия имеют происхождение от греческого языка: «до» - два, «три» - три, «тетра» - четыре, «пента» - пять. Особый интерес для среднего звена может составить «Пентамино»: составление из 5 квадратиков различных 12 простых фигур (основа игры), а затем - более сложные геометрические фигуры. Например: сложить из всех фигурок, без перекрытий и зазоров, прямоугольник и т.д.

Рисунок 5. Фигуры Пентамино.

2.4. Применение геометрических головоломок в современном мире

Геометрические фигуры и наука о изучении их свойств появились в процессе деятельности человека. Можно предположить, что и элементы геометрических головоломок также участвуют в жизни современного человека.

Танграм во всех его проявлениях можно встретить начиная от дизайна одежды, заканчивая архитектурой и ландшафтным дизайном. Самое удачное применение танграма, пожалуй в качестве мебели. Вся мебель, построенная по принципу танграма, очень удобна и функциональна. Каждый раз она может видоизменятся в зависимости от настроения и желания хозяина. Сами производители выпустили вместе с инструкцией по сборке несколько страниц с идеями для библиотеки, гостиной, спальни и детской. Самое вкусное применение танграма в шоколаде. [5.6] (Приложение №2).

Результаты анкетирования и эксперимента

Были опрошены люди от 9 до 60 лет.

Вопросы анкеты:

Фамилия, имя, отчество.
Сколько Вам полных лет.
Какие геометрические головоломки Вы знаете.
Какие качества и способности, по Вашему мнению, развивают у человека занятия геометрическими головоломками.
Где в современном мире встречали геометрические головоломки. (Приложение №3)

Опрос показал, что учащиеся мало знают геометрические головоломки.

Диаграмма №1.

Анализируя данные, выяснили, что школьники начального и среднего звеньев не знают геометрических головоломок «Танграм», «Колумбово яйцо», «Полимино», только люди старшего поколения в малой степени знакомы с этими играми. Самая популярная головоломка среди населения - кубик Рубик.Дети 9-10 лет увлекаются мозаикой и пазлами, а вот подростки, кроме кубика Рубика ничего не знают.

Диаграмма №2

Все, даже младшие школьники, понимают, что геометрические головоломки развивают определенные навыки и качества у людей, т.е. занятия головоломками – не пустая трата времени. Как дети, так и взрослые в основном отмечают развитие логического и пространственного мышления, «ум». Люди от 25 лет и старше обращают внимание на то, что увлечение геометрическими головоломками формирует усидчивость, трудолюбие и внимание.

Диаграмма №3

Оказалось, что многие (от 20 – 40% анкетируемых) не видели и не знают, где можно встретить в современном мире применение геометрических головоломок «Танграм», «Колумбово яйцо», «Полимино» и т.д. Остальные отмечают их использование в детских играх, мебели, различных орнаментах, в архитектуре, в журналах и газетах.

В ходе исследования нами проведён эксперимент, в ходе которого на переменах школьникам предложены механические (геометрические) головоломки. Результаты эксперимента показали невысокий уровень заинтересованности школьников в решении геометрических головоломок ( 14 % подростков).

Выводы

Проведенное исследование показывает, что взрослые люди мало интересуются и увлекаются геометрическими головоломками, дети же о «Танграм», «Колумбово яйцо» и «Полимино» совсем не знают. Это означает, что в дошкольных учреждениях и в начальной школе не используют задания геометрических головоломок либо не говорят, как называется данная игра. Все участники анкетирования отмечают положительное влияние занятий геометрическими головоломками на развитие умственных способностей у человека.

В ходе работы:

Определены виды головоломок.
Изучена история появления отдельных типов головоломок.
Изучены правила игр.
Выявлено применение геометрических головоломок в современном мире.
Проведен опрос населения, с целью выявления степени знания и увлеченности геометрическими головоломками;
Проведен эксперимент среди школьников;
Систематизированы полученные данные в диаграммах и сделаны выводы.

В ходе исследования доказано, что учащиеся и взрослые люди мало знают о геометрических головоломках и мало ими увлекаются.

Перспектива дальнейшего исследования – реализация проекта «Геометрические головоломки в школе», цель которого – внедрение геометрических головоломок во внеурочную деятельность школьников.

Список использованной литературы и источников

Головин, Д. А., Дубровский Е. Э., Ловков К. И., Шамшурина Ю. С., Ястребов М. И., Шмелева О. В. Математические головоломки: полимино. // Юный ученый. — 2016. — №6.1. — С. 21-23.
Ефремов, Т.В. Новый словарь русского языка. Толково – словообразовательный словарь.: Ок.160 000 слов/ Т.В. Ефремов – М.: Дрофа, 2000. – 1233с
Муравин, Г.К. Математика. 5 кл..: учеб. для общеобразовательных учреждений/ Г.К. Муравин, О.В. Муравина. – 3-е издю, перераб. – М.: Дрофа, 2007.-315с.: ил.
Ожегов,С.И. Словарь русского языка: Ок.53 000 слов/ С.И. Ожегов; Под общ. ред. проф. Л.И. Скворцова – М.: ООО «Издательство Оникс», 2011. – 1200с.
Интернет - ресурсы:

http://razvitiedetei.info/dosug/geometricheskij-konstruktor-tangram.html- Детский сайт для родителей. Развитие детей.
https://ncuxolog.ru/zagadochnyj-tangram- Мир детских эмоций и чувств.
https://ru.wikipedia.org/wiki-ВикипедиЯ
http://fb.ru/article/173523/kolumbovo-yaytso-uvlekatelnaya-golovolomka-dlya-detey-i-vzroslyih - Fb.ru
http://novijmir.blogspot.ru/p/blog-page_17.html-Волшебная шкатулка. Занимательная математика.
https://www.livemaster.ru/topic/463495-v-mire-tangram-igrushka-na-vse-vremena- журнал «Ярмарка мастеров»
http://fitnessbrain.ru/golovolomki/golovolomka - Прокачай свой мозг. Фитнес – клуб для мозга.

Приложение №1

Фигуры головоломки «Танграм», составленные учащимися 6 класса МКОУ «Брылинская СОШ»

Приложение №2

Примеры применение «Танграма» в современной жизни человека

Приложение №3

kopilkaurokov.ru