Плоскость (в математике). Что такое плоскость в математике 5 класс определение
Плоскость (в математике) - это... Что такое Плоскость (в математике)?
Две пересекающиеся плоскости
Пло́скость — одно из основных понятий геометрии. При систематическом изложении геометрии понятие плоскости обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии. Уравнение плоскости впервые встречается у А. К. Клеро (1731), уравнение плоскости в отрезках, по-видимому, впервые встречается у Г.Ламе (1816—1818), нормальное уравнение ввёл Л. О. Гессе (1861).
Некоторые характеристические свойства плоскости
- Плоскость — поверхность, содержащая полностью каждую прямую, соединяющую любые её точки;
- Плоскость — множество точек, равноотстоящих от двух заданных точек.
Аналогично отрезку и интервалу, плоскость не включающую крайние точки можно назвать интервальной плоскостью или открытой плоскостью.
Уравнения плоскоcти
Плоскость — алгебраическая поверхность первого порядка: в декартовой системе координат плоскость может быть задана уравнением первой степени.
- Общее уравнение (полное) плоскости
где A,B,C и D — постоянные, причём A,B и C одновременно не равны нулю; в векторной форме:
где — радиус-вектор точки M(x,y,z), вектор перпендикулярен к плоскости (нормальный вектор). Направляющие косинусы вектора :
Если один из коэффициентов в уравнении П. равен нулю, уравнение называется неполным. При D = 0 П. проходит через начало координат, при A = 0 (или B = 0, C = 0) П. параллельна оси Ox (соответствённо Oy или Oz). При A = B = 0 (A = C = 0, или B = C = 0) П. параллельна плоскости Oxy (соответственно Oxz или Oyz).
- Уравнение плоскости в отрезках:
где a = − D / A,b = − D / B,c = − D / C — отрезки, отсекаемые П. на осях Ox,Oy и Oz.
- Уравнение плоскости, проходящей через точку M(x0,y0,z0) перпендикулярно вектору нормали :
в векторной форме:
- Уравнение плоскости, проходящей через три заданные точки M(xi,yi,zi), не лежащие на одной прямой:
(смешанное произведение векторов), иначе
- Нормальное (нормированное) уравнение плоскости
в векторной форме:
где - единичный вектор, p — расстояние П. от начала координат. Уравнение (2) может быть получено из уравнения (1) умножением на нормирующий множитель
(знаки μ и D противоположны).
Расстояние от точки до плоскости
Расстояние от точки до плоскости — это наименьшее из расстояний между этой точкой и точками плоскости. Известно, что расстояние от точки до плоскости равно длине перпендикуляра, опущенного из этой точки на плоскость.
- Отклонение точки M1(x1,y1,z1) от плоскости заданной нормированным уравнением (2)
- Расстояние ρ от точки M0(x0,y0,z0), до плоскости, заданной уравнением ax + by + cz + d = 0, вычисляется по формуле:
Расстояние между параллельными плоскостями
- Расстояние между плоскостями, заданными уравнениями Ax + By + Cz + D1 и Ax + By + Cz + D2:
- Расстояние между плоскостями, заданными уравнениями и :
Связанные понятия
- Угол между двумя плоскостями. Если уравнения П. заданы в виде (1), то
Если в векторной форме, то
или- Плоскости перпендикулярны, если
- Пучок плоскостей — уравнение любой П., проходящей через линию пересечения двух плокостей
где α и β — любые числа, не равные одновременно нулю.
Плоскости в четырёхмерном пространстве
Если в четырёхмерном пространстве две плоскости лежат в одной гиперплоскости, то они могут либо быть параллельными (в частности, совпадать), либо пересекаться по линии.
Если же две плоскости не лежат в одной гиперплоскости, то они либо не пересекаются (скрещиваются, подобно тому как в трёхмерном пространстве скрещиваются прямые), либо имеют ровно одну общую точку.
Пересечение двух плоскостей в точке (а не по линии, как в трёхмерном пространстве) можно проиллюстрировать следующим примером. Пусть дана система декартовых координат x y z t. Пусть две плоскости α и β проходят через начало координат, причём плоскость α содержит координатные прямые x и y, а плоскость β содержит координатные прямые z и t. Соответственно у всех точек плоскости α координаты z и t равны 0, а у всех точек плоскости β координаты x и y равны 0. Тогда очевидно, что единственная точка, которая может принадлежать обеим плоскостям — это точка (0,0,0,0).
Литература
Ильин В. А., Позняк Э. Г. Аналитическая геометрия. — М.: ФИЗМАТЛИТ, 2002. — 240 с.
Wikimedia Foundation. 2010.
dic.academic.ru
Что такое плоскость?
Геометрия – это предмет, который все мы начинаем изучать еще в школе, это то, что окружает нас повсюду - точки и прямые, объемные и плоские фигуры. Геометрия начинается с самых простых и основных фигур: точка, прямая и плоскость. В этой статье разберем, что такое плоскость.
Понятие «плоскости»
Понятие плоскости не имеет четкого определения, это поверхность, начало и конец которой нельзя увидеть. Таким образом, плоскость следует представлять безгранично простирающейся во все стороны. Аксиомы геометрии определяют плоскость лишь косвенно.
Для простоты и большего понимания плоскость в геометрии рассматривается частично, т. е. только та её часть, которая ограничена ломаной замкнутой линией. Мы можем видеть такую часть плоскости в форме эллипса, прямоугольника, круга или многоугольника.
В качестве примера можно привести множество вариантов – это потолок комнаты, поверхность стола, лист бумаги или любая другая гладкая поверхность.
Аксиомы, определяющие плоскость и её свойства
- Плоскость – это место в пространстве, поверхность, которая содержит полностью любую прямую, что соединяет любые точки плоскости.
- Любые две плоскости по отношению друг к другу либо параллельны, либо пересекаются по какой-либо прямой.
- Прямая может находиться в трех положениях:
- быть параллельной плоскости;
- пересекать плоскость в какой-то точке;
- быть расположенной на самой плоскости.
- Две прямые, которые перпендикулярны определенной плоскости, параллельны между собой.
- Две плоскости, которые перпендикулярны определенной прямой, параллельны между собой.
Уравнение плоскости
Общее уравнение плоскости было введено Л. О. Гессе в 1861 году, хотя впервые упоминания об этом уравнении можно встретить в работах А. К. Клеро еще в 1731 году.
Итак, выглядит это уравнение следующим образом:
где: A, B, C и D – это постоянные числа, причем, первые три из них одновременно не равны 0.
Как проверить взаимное расположение плоскостей
Имея две плоскости и два их уравнения, можно легко проверить, как они расположены по отношению друг к другу. Для этого выведены равенства, в которые просто необходимо будет подстав
elhow.ru
Плоскость (математика) - это... Что такое Плоскость (математика)?
Плоскость (математика)
У этого термина существуют и другие значения, см. Плоскость. Две пересекающиеся плоскостиПло́скость — одно из основных понятий геометрии. При систематическом изложении геометрии понятие плоскости обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии. Уравнение плоскости впервые встречается у А. К. Клеро (1731), уравнение плоскости в отрезках, по-видимому, впервые встречается у Г.Ламе (1816—1818), нормальное уравнение ввёл Л. О. Гессе (1861).
Некоторые характеристические свойства плоскости
- Плоскость — поверхность, содержащая полностью каждую прямую, соединяющую любые её точки;
- Плоскость — множество точек, равноотстоящих от двух заданных точек.
Аналогично отрезку и интервалу, плоскость не включающую крайние точки можно назвать интервальной плоскостью или открытой плоскостью.
Уравнения плоскоcти
Плоскость — алгебраическая поверхность первого порядка: в декартовой системе координат плоскость может быть задана уравнением первой степени.
- Общее уравнение (полное) плоскости
где A,B,C и D — постоянные, причём A,B и C одновременно не равны нулю; в векторной форме:
где — радиус-вектор точки M(x,y,z), вектор перпендикулярен к плоскости (нормальный вектор). Направляющие косинусы вектора :
Если один из коэффициентов в уравнении П. равен нулю, уравнение называется неполным. При D = 0 П. проходит через начало координат, при A = 0 (или B = 0, C = 0) П. параллельна оси Ox (соответствённо Oy или Oz). При A = B = 0 (A = C = 0, или B = C = 0) П. параллельна плоскости Oxy (соответственно Oxz или Oyz).
- Уравнение плоскости в отрезках:
где a = − D / A, b = − D / B, c = − D / C — отрезки, отсекаемые П. на осях Ox,Oy и Oz.
- Уравнение плоскости, проходящей через точку M(x0,y0,z0) перпендикулярно вектору нормали :
в векторной форме:
- Уравнение плоскости, проходящей через три заданные точки M(xi,yi,zi), не лежащие на одной прямой:
(смешанное произведение векторов), иначе
- Нормальное (нормированное) уравнение плоскости
в векторной форме:
где - единичный вектор, p — расстояние П. от начала координат. Уравнение (2) может быть получено из уравнения (1) умножением на нормирующий множитель
(знаки μ и D противоположны).
Расстояние от точки до плоскости
Расстояние от точки до плоскости — это наименьшее из расстояний между этой точкой и точками плоскости. Известно, что расстояние от точки до плоскости равно длине перпендикуляра, опущенного из этой точки на плоскость.
- Отклонение точки M1(x1,y1,z1) от плоскости заданной нормированным уравнением (2)
- Расстояние ρ от точки M0(x0,y0,z0), до плоскости, заданной уравнением ax + by + cz + d = 0, вычисляется по формуле:
Расстояние между параллельными плоскостями
- Расстояние между плоскостями, заданными уравнениями Ax + By + Cz + D1 и Ax + By + Cz + D2:
- Расстояние между плоскостями, заданными уравнениями и :
Связанные понятия
- Угол между двумя плоскостями. Если уравнения П. заданы в виде (1), то
Если в векторной форме, то
или- Плоскости перпендикулярны, если
- Пучок плоскостей — уравнение любой П., проходящей через линию пересечения двух плокостей
где α и β — любые числа, не равные одновременно нулю.
Плоскости в четырёхмерном пространстве
Если в четырёхмерном пространстве две плоскости лежат в одной гиперплоскости, то они могут либо быть параллельными (в частности, совпадать), либо пересекаться по линии.
Если же две плоскости не лежат в одной гиперплоскости, то они либо не пересекаются (скрещиваются, подобно тому как в трёхмерном пространстве скрещиваются прямые), либо имеют ровно одну общую точку.
Пересечение двух плоскостей в точке (а не по линии, как в трёхмерном пространстве) можно проиллюстрировать следующим примером. Пусть дана система декартовых координат x y z t. Пусть две плоскости α и β проходят через начало координат, причём плоскость α содержит координатные прямые x и y, а плоскость β содержит координатные прямые z и t. Соответственно у всех точек плоскости α координаты z и t равны 0, а у всех точек плоскости β координаты x и y равны 0. Тогда очевидно, что единственная точка, которая может принадлежать обеим плоскостям — это точка (0,0,0,0).
Литература
Ильин В. А., Позняк Э. Г. Аналитическая геометрия. — М.: ФИЗМАТЛИТ, 2002. — 240 с.
dic.academic.ru
Точка, отрезок, луч, прямая - числовая прямая
Мы рассмотрим каждую из тем, а в конце будут даны тесты по темам.
Точка в математике
Что такое точка в математике? Математическая точка не имеет размеров и обозначается заглавными латинскими буквами: A, B, C, D, F и т.д.
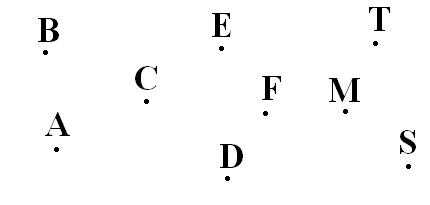
На рисунке можно видеть изображение точек A, B, C, D, F, E, M, T, S.
Отрезок в математике
Что такое отрезок в математике? На уроках математики можно услышать следующее объяснение: математический отрезок имеет длину и концы. Отрезок в математике - это совокупность всех точек, лежащих на прямой между концами отрезка. Концы отрезка - две граничные точки.
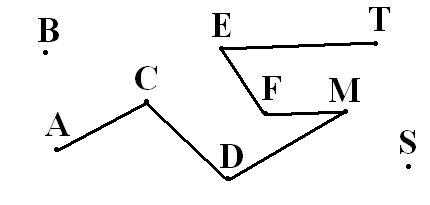
На рисунке мы видим следующее: отрезки [A;C],[C;D],[D;M],[M;F],[F;E] и [E;T], а также две точки B и S.
Прямая в математике
Что такое прямая в математике? Определение прямой в математике: прямая не имеет концов и может продолжаться в обе стороны до бесконечности. Прямая в математике обозначается двумя любыми точками прямой. Для объяснения понятия прямой ученику можно сказать, что прямая - это отрезок, который не имеет двух концов.
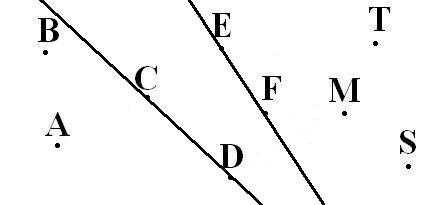
На рисунке изображены две прямые: CD и EF.
Луч в математике
Что же такое луч? Определение луча в математике: луч - часть прямой, которая имеет начало и не имеет конца. В названии луча присутствуют две буквы, например, DC. Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.
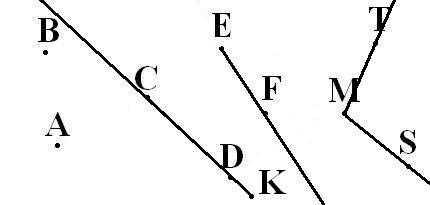
На рисунке изображены лучи: DC, KC, EF, MT, MS. Лучи KC и KD - один луч, т.к. у них общее начало.
Числовая прямая в математике
Определение числовой прямой в математике: прямая, точки которой отмечают числа, называют числовой прямой.
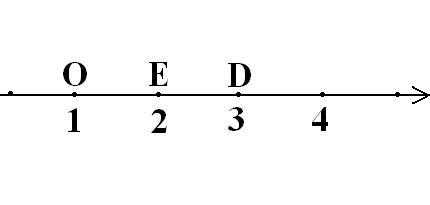
На рисунке изображена числовая прямая, а также луч OD и ED
Нужна помощь в учебе?
Предыдущая тема: Сложение и вычитание дробей с одинаковыми знаменателями: ПРИМЕРЫ Следующая тема:   Чтение и запись больших натуральных чисел: разряды, классы + ПРИМЕРВсе неприличные комментарии будут удаляться.
www.nado5.ru
Плоскость (геометрия) - это... Что такое Плоскость (геометрия)?
 Две пересекающиеся плоскости
Две пересекающиеся плоскости Пло́скость — одно из основных понятий геометрии. При систематическом изложении геометрии понятие плоскости обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии.
Некоторые характеристические свойства плоскости
- Плоскость — поверхность, содержащая полностью каждую прямую, соединяющую любые её точки;
- Две плоскости являются либо параллельными, либо пересекаются по прямой.
- Прямая либо параллельна плоскости, либо пересекает ее в одной точке, либо находится на плоскости.
- Две прямые, перпендикулярные одной и той же плоскости, параллельны друг другу.
- Две плоскости, перпендикулярные одной и той же прямой, параллельны друг другу.
Аналогично отрезку и интервалу, плоскость, не включающую крайние точки, можно назвать интервальной плоскостью, или открытой плоскостью.
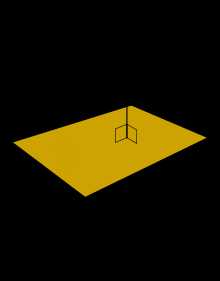 Плоскость и два её нормальных вектора: n1 и n2
Плоскость и два её нормальных вектора: n1 и n2 Уравнения плоскости
Впервые встречается у А. К. Клеро (1731).
Уравнение плоскости в отрезках, по-видимому, впервые встречается у Г.Ламе (1816—1818).
Нормальное уравнение ввёл Л. О. Гессе (1861).
Плоскость — алгебраическая поверхность первого порядка: в декартовой системе координат плоскость может быть задана уравнением первой степени.
- Общее уравнение (полное) плоскости
где и — постоянные, причём и одновременно не равны нулю; в векторной форме:
где — радиус-вектор точки , вектор перпендикулярен к плоскости (нормальный вектор). Направляющие косинусы вектора :
Если один из коэффициентов в уравнении плоскости равен нулю, уравнение называется неполным. При плоскость проходит через начало координат, при (или , ) П. параллельна оси (соответственно или ). При (, или ) плоскость параллельна плоскости (соответственно или ).
- Уравнение плоскости в отрезках:
где , , — отрезки, отсекаемые плоскостью на осях и .
- Уравнение плоскости, проходящей через точку перпендикулярно вектору нормали :
в векторной форме:
- Уравнение плоскости, проходящей через три заданные точки , не лежащие на одной прямой:
(смешанное произведение векторов), иначе
- Нормальное (нормированное) уравнение плоскости
в векторной форме:
где - единичный вектор, — расстояние П. от начала координат. Уравнение (2) может быть получено из уравнения (1) умножением на нормирующий множитель
(знаки и противоположны).
Определение по точке и вектору нормали
В трехмерном пространстве одним из важнейших способов определения плоскости является указание точки на плоскости и вектора нормали к ней.
Допустим, является радиусом-вектором точки , заданной на плоскости, и допустим, что n - это ненулевой вектор, перпендикулярный к плоскости (нормаль). Идея состоит в том, что точка с радиусом-вектором r находится на плоскости тогда и только тогда, когда вектор, проведённый от к , перпендикулярен n.
Вернёмся к тому, что два вектора являются перпендикулярными тогда и только тогда, когда их скалярное произведение равно нулю. Отсюда следует, что нужная нам плоскость может быть выражена как множество всех точек r таких, что:
(Здесь точка означает скалярное произведение, а не умножение.)Развернув выражение, мы получим:
что является знакомым нам уравнением плоскости.
Например: Дано: точка на плоскости и вектор нормали .
Уравнение плоскости записывается так:
Расстояние от точки до плоскости
Расстояние от точки до плоскости — это наименьшее из расстояний между этой точкой и точками плоскости. Известно, что расстояние от точки до плоскости равно длине перпендикуляра, опущенного из этой точки на плоскость.
- Отклонение точки от плоскости заданной нормированным уравнением
- Расстояние от точки , до плоскости, заданной уравнением , вычисляется по формуле:
Расстояние между параллельными плоскостями
- Расстояние между плоскостями, заданными уравнениями и :
- Расстояние между плоскостями, заданными уравнениями и :
Связанные понятия
- Угол между двумя плоскостями. Если уравнения П. заданы в виде (1), то
Если в векторной форме, то
или (Векторное произведение)- Плоскости перпендикулярны, если
- Пучок плоскостей — все плоскости, проходящие через линию пересечения двух плоскостей. Уравнение пучка плоскостей, то есть любой плоскости, проходящей через линию пересечения двух плоскостей, имеет вид[1]:222:
- Связка плоскостей — все плоскости, проходящие через точку пересечения трёх плоскостей[1]:224. Уравнение связки плоскостей, то есть любой плоскости, проходящей через точку пересечения трёх плоскостей, имеет вид:
N-плоскость в пространстве
Пусть дано n-мерное аффинный-точененое пространство , над полем действительных чисел. В нём выбрана прямоугольная система координат . m-плоскостью называется множество точек , радиус векторы которых удовлетворяют следующему соотношению - матрица, столбцы которой образует направляющие подпространство плоскости, - вектор переменных, - радиус-вектор одной из точек плоскости.Указанное соотношение можно из матрично-векторного вида перевести в векторный: - векторное уравнение m-плоскости.Вектора образуют направляющее подпространство. Две m-плоскости называются параллельными, если их направляющие пространства совпадают и .
(n-1)-плоскость в n-мерном пространстве называется гиперплоскостью или просто плоскостью. Для гиперплоскости существует общее уравнение плоскости. Пусть - нормальный вектор плоскости, - вектор переменных, - радиус вектор точки, принадлежащей плоскости, тогда: - общее уравнение плоскости.Имя матрицу направляющих векторов, уравнение можно записать так: , или:.Углом между плоскостями называется наименьший угол между их нормальными векторами.
Примеры m-плоскостей
- Примером 1-плоскости в трёхмерном пространстве (n=3) служит прямая. Её векторное уравнение имеет вид: . В случае n = 2 прямая является гиперплоскостью.
- Гиперплоскостью в трёхмерном пространстве соответствует привычному понятию плоскости.
См. также
Примечания
Литература
Ильин В. А., Позняк Э. Г. Аналитическая геометрия. — М.: ФИЗМАТЛИТ, 2002. — 240 с.
Ссылки
dic.academic.ru
ПЛОСКОСТЬ - это... Что такое ПЛОСКОСТЬ?
ПЛОСКОСТЬ — ПЛОСКОСТЬ, плоскости, мн. плоскости, плоскостей, жен. 1. только ед. отвлеч. сущ. к плоский (книжн.). Плоскость груди. Плоскость острот. 2. Поверхность, имеющая только два измерения, так что между любыми двумя точками ее можно провести прямую,… … Толковый словарь Ушакова
плоскость — См … Словарь синонимов
плоскость X-Y — горизонтальная плоскость Плоскость, определяемая осями X и Y [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы горизонтальная плоскость EN X Y plane … Справочник технического переводчика
ПЛОСКОСТЬ — простейшая поверхность. Понятие плоскость (подобно точке и прямой) принадлежит к числу основных понятий геометрии. Плоскость обладает тем свойством, что любая прямая, соединяющая две ее точки, целиком принадлежит ей … Большой Энциклопедический словарь
Плоскость — период времени, в котором цена не повышается и не падет. Плоскость период времени, когда закрыты все позиции. По английски: Flat См. также: Тренды Финансовый словарь Финам … Финансовый словарь
плоскость U — U плоскость обрабатывает данные пользователя, проходящие через систему G PON. U плоскость обеспечивает связь между клиентами ATM или клиентами GEM (МСЭ Т G.984.3). [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики… … Справочник технического переводчика
ПЛОСКОСТЬ — ПЛОСКОСТЬ, простейшая поверхность такая, что любая прямая, проходящая через 2 ее точки, принадлежит ей … Современная энциклопедия
ПЛОСКОСТЬ — ПЛОСКОСТЬ, и, мн. и, ей и ей, жен. 1. см. плоский. 2. (ей). В геометрии: поверхность, имеющая два измерения. Линия на плоскости. 3. (ей). Ровная, гладкая поверхность. По наклонной плоскости катиться (также перен.: опускаться в нравственном… … Толковый словарь Ожегова
плоскость — плоскость, мн. плоскости (неправильно плоскостя), род. плоскостей и плоскостей … Словарь трудностей произношения и ударения в современном русском языке
плоскость — Поверхность, которая имеет два измерения. Особо выделяют: плоский индикатор, плоский кабель. Операция окраски плоскости называется закраской. [Гипертекстовый энциклопедический словарь по информатике Э. Якубайтиса] [http://www.morepc.ru/dict/]… … Справочник технического переводчика
dic.academic.ru
плоскость - это... Что такое плоскость?
Морфология: (нет) чего? пло́скости, чему? пло́скости, (вижу) что? пло́скость, чем? пло́скостью, о чём? о пло́скости; мн. что? пло́скости, (нет) чего? пло́скостей и плоскосте́й, чему? пло́скостям и плоскостя́м, (вижу) что? пло́скости, чем? пло́скостями и плоскостя́ми, о чём? о пло́скостях и о плоскостя́х
1. Плоскостью называют воображаемую траекторию движения объёмного предмета.Плоскость орбиты. | Плоскость колебания маятника. | Прохождение Земли через плоскость колец Сатурна. | Плоскость круга небесной сферы перпендикулярна к оси мира.
2. Плоскостью называют поверхность, которая имеет два измерения и в которой любая прямая, соединяющая две её точки, целиком принадлежит ей.Пересечение плоскостей. | Разбивать плоскость на две области. | Проекция луча на плоскость. | Плоскость видимого в море горизонта всегда параллельна плоскости математического горизонта.
3. Плоскостью называется ровная поверхность чего-либо без возвышенностей и углублений.Вертикальная, горизонтальная плоскость. | Плоскость асфальта, пола, сцены.
4. Если кто-либо стоит, находится с кем-либо на (в) одной плоскости, то это означает, что кто-либо общается с кем-либо на равных.
5. Если кто-либо (что-либо) существуют в разных плоскостях, то это означает, что какие-либо люди, объекты, процессы и т. п. не влияют, не воздействуют друг на друга, существуют или развиваются изолированно, самостоятельно.
6. Если что-либо рассматривается в какой-либо плоскости, то это означает, что что-либо обсуждается кем-либо в определённой системе понятий.Духовная, теоретическая плоскость. | Субъективная, объективная плоскость. | Рассмотреть вопрос в различных плоскостях. | Перевести разговор в другую плоскость.
7. Плоскостью называется старая, всем известная шутка, неостроумное замечание.Говорить плоскости. | Не выношу плоскости. | Плоскость чьих-либо суждений.
= тривиальность, пошлость
8. Наклонная плоскость — это приспособление в виде покатой поверхности для подъёма и спуска тяжестей.
9. Если кто-либо катится по наклонной плоскости, то это означает, что этот человек быстро деградирует, опускается в моральном плане.
• плоскостно́й
dic.academic.ru