Дидактические математические игры для дошкольников. Дидактические математические игры

Дидактические игры на уроках математики для 1-4 классов.

Муниципальное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа №4 города Агрыз Агрызского

муниципального района Республики Татарстан

СБОРНИК ДИДАКТИЧЕСКИХ ИГР ПО МАТЕМАТИКЕ

1-4 классы

составитель:

учитель начальных классов

Мусина Светлана Исрафилевна

2017 год

Содержание:

Введение
Дидактическая игра, как средство активизации
Дидактический игры по математике
Заключение

ВВЕДЕНИЕ

Игра – это жизненная лаборатория детства,

дающая тот аромат, ту атмосферу молодой

жизни, без которой эта пора ее была бы бес-

полезна для человечества. В игре, этой специ-

альной обработке жизненного материала,

есть самое здоровое ядро разумной школы

детства.

С. Т. Шацкий

Проходит время, ребенок подрастает, и вот ему уже пора идти в первый класс. В школе ему придется столкнуться с множеством трудностей, получить огромное количество новых впечатлений, приобрести принципиально иной, чем в семье опыт общения. Все это требует немало усилий как умственных, так и эмоциональных. Процесс овладения новыми знаниями и навыками будет протекать для ребенка легче и эффективнее, если педагоги смогут внести в него определенную долю игры. Эта форма умственной деятельности является для ребенка привычной, а потому помогает ему справиться с трудностями, ожидающими его в первые годы обучения.

Игра является основным видом деятельности ребенка, начиная практически от рождения. Вообще термин «игра» включает в себя разнообразные виды деятельности. Именно она играет большую роль в формировании и развитии умственных, эмоциональных, физических и творческих способностей ребенка. Игра помогает развивать память, мышление, воображение, внимание. Одиночная игра развивает индивидуальные качества ребенка, знакомит его с характеристиками и свойствами тех или иных предметов. Игра в группе приучает ребенка к общественной жизни, социальным ролям и отношениям между людьми. Ролевые игры помогают ученику осваивать нормы и стереотипы поведения в современном обществе. Таким образом, можно дать игре четкое определение. Игра представляет собой вид деятельности, в которой человек добровольно принимает участие и получает удовольствие и возможность исследовательского поведения.

Игра — самый древний способ передачи знаний от поколения к поколению. Девочки играют в куклы, чтобы подготовиться к роли жены и матери, мальчики — в машинки, чтобы стать главным автолюбителем в семье. И только школьные учителя предпочитают игре с учениками серьезную дидактику. Почему же? Очевидно, потому, что в многочисленных определениях игровой деятельности подчеркивается отсутствие практической направленности, ориентации на результат. А обучение, как учит педагогика, — это целенаправленная деятельность, которую учитель по роду своей профессии призван организовывать. Однако это противоречие снимается, как только мы добавляем понятие «дидактическая», «педагогическая» игровая деятельность, ибо в таком случае цель задается учителем.

Интерес детей в дидактической игре перемещается от игрового действия к умственной задаче. Дидактическая игра является ценным средством воспитания умственной активности детей, она активизирует психические процессы, вызывает у учащихся живой интерес к процессу познания. В ней дети охотно преодолевают значительные трудности, тренируют свои силы, развивают способности и умения. Она помогает сделать любой учебный материал увлекательным, вызывает у учеников глубокое удовлетворение, создает радостное рабочее настроение, облегчает процесс усвоения знаний.

В дидактических играх ребенок наблюдает, сравнивает, сопоставляет, классифицирует предметы по тем или иным признакам, производит доступные ему анализ и синтез, делает обобщения.

Форма проведения игры может быть разной:

Игровая деятельность как элемент урока может применяться на любом этапе его — от проверки домашнего задания до выполнения проверочной работы и обобщения.

В основе предлагаемых материалов лежит идея использования в обучении младших школьников игр. В игре для ребенка появляется возможность добывать знания самостоятельно; он ощущает радость успеха и уверенность в своих силах. Каждый педагог может найти несколько минут в учебном дне для того, чтобы окунуться с младшими школьниками в игровую деятельность. Игры повышают эмоциональный тонус школьника, а без положительных эмоций не может быть плодотворной учебной деятельности. Использование игровых технологий несомненно даст заметный эффект в развитии детей, а также, улучшит эмоциональное состояние детей, поддержит у младших школьников интерес к учебной деятельности, минуя неблагоприятные тенденции школьного обучения.

Дидактические игры на уроках математики.

1.Бабочки.

Дидактическая цель. Закреплять приемы прибавления и вычитания

Оборудование. Рисунки бабочек и цветов.

Содержание. На доске цветы с числом, бабочки группой на другой части доски. Детям предлагают отгадать, на какой цветок сядет бабочка. Для этого они читают примеры на обратной стороне рисунков бабочек и считают его, затем сажают бабочек на цветы.

2. Математический футбол.

Дидактическая цель. Формировать навыки сложения и вычитания в пределах 20, 100, 1000 или умножения и деления.

Оборудование. Картинки ворот, мячей с примерами.

Содержание. На доске ворота, дети разделились на 2 команды. Выбегают по очереди, берут мяч, с обратной стороны написан пример, если решил правильно – то забил гол. Побеждает тот, кто считает без ошибок и больше забил мячей.

3. Математическая рыбалка.

Дидактическая цель. Формировать и закреплять навыки устного счета в 1-4 классах.

Оборудование. Рыбки и рыбак

Содержание. Играют команды, по очереди берут рыбку и решают пример. Решил правильно - поймал рыбку. Кто больше наловит.

Можно примеры писать с обратной стороны рыбок.

4. Новогодняя елочка

Оборудование. Елочка, картинки Деда Мороза и Снегурочки, елочные игрушки.

Цель. Отработка и проверка навыка счета.

Содержание. Ученик Снегурочке помогает наряжать елку, если правильно решает пример, записанный на обратной стороне игрушки.

5. Поезд.

Дидактическая цель. Закрепить порядковое значение числа.

Оборудование. Картинки поезда, вагонов, карточки с числами от 1 до20.

Содержание. На доске поезд, вагоны расставлены в беспорядке. Детям объявляют, что числа заблудились. Дети расставляют цифры, обозначающие числа второго десятка.

6. Угадай.

Дидактическая цель. Закрепить знание состава чисел первого десятка.

Содержание. Учитель говорит, что задумала 2 числа, сложила их, получилось 5. Какие числа сложила? Дети: 0 и 5, 5 и 0, 4 и 1, 1 и 4, 2 и 3, 3 и 2. На первом этапе дети иллюстрируют состав чисел на палочках, на геометрических фигурах.

7. Наоборот.

Дидактическая цель. Развивать речь детей, закреплять понятия толстый, тонкий, широкий, узкий и т. д.

Содержание. Учитель говорит слово, а ребенок противоположное ему. Учитель не называет имен, а бросает мяч.

Дополнение.

Дидактическая цель. Развивать речь детей, включать в активный словарь математические термины.

Оборудование. Рисунки ракеты, самолета, вертолета, птицы, бабочки.

Содержание. Учитель на доске размещает картинки сверху вниз. Разъясняет детям, что надо продолжить предложение (Высоко в небе летит …,ниже ракеты летит …. Самолет летит выше …, ниже вертолета летит …)

8. Составим цветок.

Дидактическая цель. Закрепление состава чисел первого десятка.

Оборудование. лепестки с примерами; стебель с листом, на котором число.

Содержание игры. На доску крепят стебли с листом. Лепестки лежат на столе. Выходит ученик и берет лепесток, читает пример разными способами, решает устно и прикрепляет к нужному стеблю. Играют дети по командам: сколько цветов, столько команд.

9. Лучший космонавт.

Дидактическая цель. Формирование навыков сложения и вычитания.

Содержание игры. Учитель на доске рисует 10 ракет с номерами от 1 до 10. Вызываются сразу 11 учеников. Вокруг стола, где разложены карточки с примерами, дети идут, взявшись за руки, и декламируют: «Ждут нас быстрые ракеты На такую полетим! Для прогулок по планетам. Но в игре один секрет: На какую захотим, Опоздавшим места нет». Как только сказано последнее слово, учитель выдает каждому ученику карточки с примерами, шифрующими номер ракеты, на которой полетит космонавт. Дети решают примеры, определяя номер своей ракеты, и пишут пример под соответствующим номером ракеты.

10. Составь круговые примеры.

Дидактическая цель. Составление примеров, у которых первый компонент равен ответу предыдущего примера.

Содержание игры. Учащиеся составляют примеры с ответом, равным первому компоненту следующего примера. Например, на доске даны следующие записи: 7-5=2 2+6=8 8+2=10 10-8=2 Учащиеся составляют цепочку примеров по заданному правилу. Игру можно проводить в любом классе, усложняя задания.

11. Почтальон.

Дидактическая цель. Закрепление приемов умножения и деления (табличные случаи). Оборудование: Рисунки домиков, карточки с примерами.

Содержание игры. Учитель вызывает к доске учеников, они выбирают карточку с примером, решают, указывают номер дома, квартиры, куда отправлено письмо.

12. Математическая эстафета.

Дидактическая цель. Обучение навыкам быстрого счёта.

Содержание игры. Класс разбивается на команды. Для каждой команды учитель пишет примеры. Одновременно от каждой команды к доске вызывается по одному ученику. Их задача состоит в том, чтобы правильно и быстро решить соответствующий пример и передать эстафету своему товарищу. Игра продолжается до тех пор, пока ученики каждой команды решат все примеры. Побеждает та команда, которая раньше других правильно решит примеры

13. Молчанка.

Дидактическая цель. Закрепление навыков устного счёта.

Содержание игры. На доске или карточке записаны числа по кругу, а в центре знак действия. Учитель молча показывает на два числа и на кого-то из учащихся. Тот должен выполнить с ними определённое действие и назвать ответ. Остальные сигнализируют о правильности решения.

14. «Мальчики – Девочки»

Дидактическая цель. Развитие внимания, быстроты мыслительных операций, памяти.

Содержание игры. По щелчку на экране появляются кружки разного цвета с примерами. Задание: Если кружок синего цвета, то ответ хором называют мальчики, если красного – девочки. Выигрывают, те кто меньше допустил ошибок. Если кружок другого цвета , в классе тишина.

15. «Математическая тучка»

Дидактическая цель. Развитие внимания, зрительного восприятия, закрепление учебного материала с помощью игровой мотивации.

Содержание игры. На экране изображение тучки и капельки с числом. Задание: Дети по вызову учителя выходят к доске и подбирают к тучке пару капельку с таким же числом. Нужно навести курсор на нужную капельку и щёлкнуть.

16. «Освободи птичку»

Дидактическая цель. Обобщение знания чисел от 21 до 100.

Содержание игры. Птички находятся в клетке и учитель предлагает детям выпустить их на волю, но для этого нужно выполнить задание. Учащиеся берут птичку из клетки и с обратной стороны читают задание (например, посчитай десятками до 60, назови число, в которых 2 дес., и 6 ед., и.т.п). Если ученик правильно ответит на вопрос, то птичка летит (переставляется) на дерево, если нет, то возвращается обратно в клетку.

17. Найди и назови.

Дидактическая цель. Закрепить умение быстро находить геометрическую фигуру определённого размера и цвета.

Содержание игры. На столе перед ребёнком раскладываются в беспорядке 10-12 геометрических фигур разного цвета и размера. Ведущий просит показать различные геометрические фигуры, например: большой круг, маленький синий квадрат и т.д.

18. Только одно свойство.

Дидактическая цель. зЗкрепить знание свойств геометрических фигур, развивать умение быстро выбрать нужную фигуру, охарактеризовать её.

Содержание игры. У двоих играющих по полному набору геометрических фигур. Один кладёт на стол любую фигуру. Второй играющий должен положить на стол фигуру, отличающуюся от неё только одним признаком. Так, если 1-й положил жёлтый большой треугольник, то второй кладёт, например, жёлтый большой квадрат или синий большой треугольник. Игра строится по типу домино.

19. Назови число.

Содержание игры. Играющие становятся друг против друга. Взрослый с мячом в руках бросает мяч и называет любое число, например 7. Ребёнок должен поймать мяч и назвать смежные числа – 6 и 8 (сначала меньшее)

20. «Живой уголок»

Дидактическая цель. Ознакомление детей с приемом образования чисел при одновременном закреплении пространственной ориентации, понятий «больше», «меньше».

Содержание игры. Учитель говорит: «В нашем живом уголке живут кролики: серый и белый, кролики грызут морковь. Сколько кроликов грызут морковь? (два, ответ фиксируется показом цифры 2). Назовите, какие кролики грызут морковь? (серый и белый). К ним прибежал еще один кролик. Что изменилось? (кроликов стало больше) Сколько кроликов теперь едят морковь? (три, ответ фиксируется показом цифры 3) Перечисли их (один белый и еще один белый, и еще один серый, всего три). Каких кроликов больше, белых или серых? (белых) Почему их больше? (их два, а два это один и один). Почему 21? (два идет при счете после числа 1). Аналогично можно рассматривать образование последующих чисел.

21. «Хлопки»

Содержание игры. Учитель на магнитном моделеграфе размещает по секторам от 1 до 10 рисунков. Открывая по очереди сектор за сектором, предлагает сосчитать число рисунков и по его сигналу похлопать столько же раз, сколько открыто рисунков, и показать нужную цифру. (Учитель задает ритм хлопков).

22. «Числа, бегущие навстречу друг другу»

Дидактическая цель. Знакомство с составом числа 10.

Содержание игры. Учитель предлагает детям записать в тетради числа от 1 до 10 по порядку и дугами показать два числа, которые бегут навстречу друг другу, образуя в сумме число 10. Затем просит записать примеры на сложение с этими числами.

Например:

0 1 2 3 4 5 6 7 8 9 10

0 +10 = 10 - 10 + 0 = 10

1 + 9 = 10 - 9 + 1 = 10

Учитель спрашивает: «Что интересного вы заметили при составлении примеров? Дети отвечают, что числа, стоящие на одинаковых местах справа и слева в числовом ряду, составляют в сумме число 10»

23. «Математическая эстафета»

Дидактическая цель. Ознакомление с образованием чисел из десятка и единиц.

Оборудование. 10 кругов и 10 треугольников из приложенных к учебнику математики для 1 класса.

Содержание игры. Учитель делит класс на 3 команды по рядам и проводит игру-соревнование. Первый ученик из первой команды иллюстрирует число с помощью кругов и треугольников, второй из этой же команды называет обозначенной число, третий – его состав, четвертый показывает число на карточках. Аналогичные упражнения выполняют из второй и третий команд. Победит та команда, которая не допустит ни одной ошибки или допустит меньшее их число.

24. «Подарки Петрушки» ( состав чисел первого десятка)

Дидактическая цель. Ознакомить с составом числа 5.

Оборудование. Иллюстрации Петрушки, Незнайки и Веселого Карандаша; воздушные шары, вырезанные из цветного картона.

Содержание игры. Учитель сообщает, что на урок в гости пришел Петрушка с воздушными шарами и с ним пришли его друзья. Незнайка и Веселый Карандаш (на доску крепятся иллюстрации с изображением сказочных героев). Петрушка решил подарить шары Незнайке и Веселому Карандашу. Как он может подарить их? Дети перечисляют возможные варианты состава числа пять и иллюстрируют у доски и после записывают в тетрадь. В конце игры наиболее активные дети поощряются.

25. «Цепочка»

Содержание игры. Учитель выставляет для каждого ряда (команды) на подставку доски карточки, изображающие числа вида:

Учащиеся каждого ряда (команда) считают единицы каждого разряда и по цепочке называют проиллюстрированные числа (сначала ученик первой, потом второй и третьей команды). Потом учитель ставит другие карточки, иллюстрирующие числа второго десятка и ученики по цепочке называют их. Игра продолжается аналогично. Выигрывает команда, которая допустит меньше ошибок в образовании двузначных чисел. Для подведения итогов игры учитель отмечает в таблице звездочками правильные ответы учащихся.

26. «Контролеры»

Дидактическая цель. Закрепление знания состава чисел первого десятка.

Содержание игры. Учитель распределяет детей на две команды. Два контролера у доски следят за правильность ответов: один – первой команды, второй - другой команды. По сигналу учителя ученики первой команды делают несколько ритмических наклонов вправо, влево и считают про себя. По сигналу учителя они называют хором число наклонов первой команды до заданного числа и ведут счет про себя (например, 6 – прибавил, 1,7 – прибавил 2,8 – прибавил 3). Затем они называют число выполненных наклонов. По числу наклонов, выполненных учениками 1 и 2 группы, и называется состав числа. Учитель говорит: «Восемь – это…», ученики продолжают: «Пять и четыре». Контролеры показывают зеленые круги в правой руке, если согласны с ответом, красный - если нет. В случае ошибки упражнение повторяется. Потом учитель предлагает детям второй команды по сигналу делают несколько приседаний, а ученики первой команды дополняют приседания до заданного числа. Называется состав числа. Аналогично анализируется состав чисел на основе хлопков.

Данная игра не только систематизирует знания учеников, но и несет элементы физической разгрузки, т.к. использует физкультурные упражнения.

27. Сколько палочек в другой руке?

Дидактическая цель. Закрепление знания десятичного состава двузначного чисел.

Оборудование. Набор отдельных палочек и пучков палочек.

Содержание игры. Вызванный ученик берет пучок палочек в одну руку, а отдельные палочки – в другую руку и показывает их классу. Дети угадывают их количество и показывают карточку с соответствующим числом.

Затем задание усложняется: надо угадать, сколько отдельных палочек в руке, если в другой – пучок, и составить пример на сложение. Например, ученик взял 15 палочек, положив пучок из 10 палочек в правую руку и 5 отдельных палочек в левую. Дети составляют пример на сложение 10+5=15

28. «Стук-стук»

Дидактическая цель. Закрепление знания по нумерации чисел в пределах 20.

Оборудование.. На доске изображена таблица с двумя разрядами:

Десятки	Единицы

Содержание игры. Учитель молча стучит указкой один раз в разряде десятков и несколько раз в разряде единиц. Дети внимательно слушают и показывают учителю соответствующее число на карточке с цифрами.

29. «Назови соседей числа»

Дидактическая цель. Эта игра дает возможность каждое число первой сотни рассматривать не изолированно, а в связи с предыдущим и последующим числом.

Оборудование . Мяч или два мяча – большой и маленький (или разного цвета).

Содержание игры. Учитель бросает мяч то одному, тот другому участнику игры, а те, возвращая мяч, отвечают на вопрос учителя. Бросая мяч, учитель называет какое-либо число, например двадцать один, играющий должен назвать смежные числа –20 и 22 (обязательно сначала меньшее, потом большее).

Возможен и другой, более сложный вариант игры. Возвращая мяч, играющий должен сначала отнять от названного учителем числа единицу, потом прибавить к нему полученную разность. Например, учитель назвал число 11, а играющий должен назвать числа 10 (11-1=10) и 21 (11+10=21).

Эту игру можно провести с двумя мячами: большим и маленьким (или разного цвета). Когда учитель бросает большой мяч, то отвечающий должен, к примеру, прибавить 9 и вернуть мяч обратно, а когда маленький – то отнять 3. Здесь дети не только считают, но и развивают внимание, чтобы не перепутать действия.

30.«Кто быстрей сосчитает?» Игра развивает зоркость, внимание.

Содержание игры. На доске вывешиваются два одинаковых плаката, на которых записаны в произвольном порядке числа. Например, от 61 до 90 (от 11 до 30 и т.п.). Например, требуется назвать и указать на таблице по порядку все числа от 61 до 90. Можно соревноваться и двумя командами, по одному человеку от каждой. Затем победители соревнуются между собой и определяется лучший счетчик.

Примерный вид плаката:

90	75	71	63	66
67	82	86	68	76
87	61	73	89	81
74	88	65	77	84
80	69	78	62	70
64	83	72	79	85

Также на этапе закрепления можно предложить следующие игры:

31.«Загадка»

Дидактическая цель. Закрепить нумерацию чисел в пределах 100; десятичный состав числа.

Содержание игры. Учитель загадывает загадку «Серебристая пила в небе ниточку вила. Кто же смелый нитью белой небо шил, да поспешил: хвост у нитки распушил?». Замени число десятками и единицами и в таблице найди буквы. Прочитайте слово и запишите его.

	5 ед.	6 ед.	7 ед.
3 дес.	К	Д	Ч
7 дес.	Т	Л	М
9 дес.	И	Ю	Ё

Ответ: летчик.

32.«Гном»

Дидактическая цель. Закрепить умение детей заменять двузначное число суммой его разрядных слагаемых.

Содержание игры. Помоги гному найти дорогу к дому. Куда идти: вперед или назад – об этом числа говорят. Замени каждое число суммой разрядных слагаемых и в таблице найди букву. Составь слово, прочитай.

	4	5	7
80	В	Ё	П
50	Д	Р	М
20	О	О	Е

Ответ: вперед.

33.«Сбежавшие числа»

Дидактическая цель. Усвоение порядка следования чисел в натуральном ряду.

Оборудование. Таблички числами.

Учитель вывешивает на доску готовые таблицы (или чертит их на доске), в пустые клетки которых надо вписать пропущенные числа. Ученики должны определить закономерность в записи цифр и вписать нужные. Учитель говорит: «Здесь каждое число живет в своем домике. Но вы видите, что некоторые домики пусты – из них сбежали числа. Какие это числа? Надо подумать и вернуть беглецов в свои дома». Выигрывает тот, кто вставит числа правильно.

Заключение.

Дидактическая игра содействует лучшему пониманию математической сущности вопроса, уточнению и формированию математических знаний учащихся. Игры можно использовать на разных этапах усвоения знаний: на этапах объяснения нового материала, его закрепления, повторения, контроля. Игра позволяет включить в активную познавательную деятельность большее число учащихся. Она должна в полной мере решать как образовательные задачи урока, так и задачи активизации познавательной деятельности, и быть основной ступенью в развитии познавательных интересов учащихся. Игра помогает учителю донести до учащихся трудный материал в доступной форме. Отсюда можно сделать вывод о том, что использование игры необходимо при обучении детей младшего школьно возраста.

Литература.

1. Журналы «Начальная школа»

2. Волкова С.И. Тетрадь с математическими заданиями. – М.: Просвещение

3. Федин С. Н. Веселые игры и головоломки. От 4 до 9 лет. – М.: Айрис-пресс

4. Кудыкина Н.В. дидактические игры и занимательные задачи.

5. Жикалкина Т.К. Система игр на уроках математики в 1 и 2 классах четырехлетней начальной школы. – М.: Новая школа

6.Уткина Н.Г.,Улитина Н.В., Юдачева Т.В.Дидактический материал по математике. АРКТИ, 2001

kopilkaurokov.ru

Дидактические игры по математике для дошкольников ⋆ Планета Детства

Дидактическая игра «Веселые цифры»

«Веселые цифры»

Предлагаю вашему вниманию занимательную игру для детей дошкольного возраста, при помощи которой ребенок научится «записывать» цифры, развивать зрительное восприятие и мелкую моторику рук.Назначение. Для родителей, воспитателей детского сада, используется в свободной и индивидуальной игровой деятельности.Дидактическая задача:

Учить выкладывать цифру по образцу;
Развивать зрительное восприятие, мелкую моторику рук;
Воспитывать умение доводить начатое дело до конца, радоваться своему успеху.

Материал:Карточки с изображением цифр (от 0 — 9) ; цветные кружочки для наложения.

Руководство:В игре могут принимать участие все дети группы или по усмотрению педагога для индивидуальной работы с целью ознакомления и закрепления написания цифр. Дети рассматривают карточку с цифрой – образцом, и накладывают цветные кружочки (можно по цвету) на них, способом наложения находят нужную форму. Если кружочки совпадают с плоскостной цифрой, задание выполнено правильно.

Пособие для работы с составом числа

Описание алгоритма изготовления пособия

Изготавливаю пособие для работы с составом числа.Для этого использую тетрадь на пружине, универсальные салфетки.

Разрезаю тетрадь на три части, предварительно уменьшив листы.Из салфеток изготавливаю различные геометрические фигуры.

В средней части у меня цифры от 2 до 10, по бокам наклеены фигуры, так же в разном количестве.

Задачи, которые помогает решить данное пособие.Пособие можно использовать при обучении детей счетной деятельности, изучении состава числа, при решении арифметических задач.

Вариант использования пособия.На начальном этапе дети работают с фигурами, считая их. При усложнении только с цифрами.Это пособие очень хорошо подходит как для индивидуальной, так и групповой работе при работе с составом числа.В этом пособии так же закрепляются названия геометрических фигур. Его можно так же использовать для сложения и вычитание цифр.

Дидактическая игра «Волшебные пазлы»

Предлагаю вашему вниманию авторскую дидактическую игру «Волшебные пазлы» Сделанную из подручных материалов: медицинских деревянных шпателей и клейкой бумаги

Функции дидактической игры: способствует активации мыслительной деятельности учащихся, вызывает у детей живой интерес и помогает усвоить учебный материал. Учит наблюдать, сравнивать, делать обобщение.

В данной игре мы закрепляем геометрические фигуры и закрепляем цвет. Так же можно наклеивать любые другие картинки в зависимости от занятия.

В этой игре у детей так же формируются психические процессы, развиваются внимание и память.

Автор: Новикова Мария Олеговна,МБДОУ ЦРР детский сад № 100,г. Владимир

Статья размещена в авторской редакци

planetadetstva.net

Дидактические игры на уроках математики

ДИДАКТИЧЕСКИЕ ИГРЫ НА УРОКАХ МАТЕМАТИКИ

Проблема образования сводится не только к передаче учащимся определенной суммы знаний и навыков по предмету, но и реализации возможностей каждого предмета в развитии личности ребенка. “Отношение учащихся к математике характеризуется в основном снижением ее популярности… Вообще, 5-6 классы – “критический возраст” в математическом развитии. Стремление добиваться владения учащимися необходимыми вычислительными навыками, делает учебу однообразной, а курс математики не интересным.

Требуются сейчас иные, не традиционные подходы к формированию знаний, выработке умения усваивать их как можно эффективнее в одну и ту же единицу времени. От того как учителю удается:

1. пробудить потребность в познании

2. вызвать интерес учащихся к предмету, во многом зависят результаты обучения и воспитания.

В.А.Сухомлинский не раз напоминал о том, что каждый нормальный ребенок идет в школу с горячим желанием учиться, с огоньком любознательности и интереса. Очень важно сохранить этот интерес и пронести его через все школьные годы.

Среди различных путей воспитания у школьников интереса к учению одним из наиболее эффективных является организация их игровой деятельности на уроке.

Игра, учение. Труд являются основными видами деятельности человека. При этом игра готовит ребенка к учению и к труду. Глубоко ошибаются те, кто считает игру лишь забавой и развлечением. Дидактические игры хорошо уживаются с серьезным учением, т.к. они облегчают преодоление трудностей в усвоении учебного материала.

Урок – это живой творческий процесс, а всякому живому чужды статичность и однообразие. Урок должен рождаться каждый раз как маленькое чудо, вызывать удивление, открытие, удовлетворение. Это особенно важно в подростковом возрасте, когда еще формируются и определяются интересы к тому или иному предмету. Именно в этот период нужно стремиться раскрыть привлекательность изучаемого предмета. Этому способствует дидактическая игра на уроке математики, обладающая образовательной, развивающей и воспитательной функциями. На таких уроках вырабатывается внимание, сосредоточенность, умение самостоятельно мыслить, появляется тяга к знаниям, пополняется запас представлений, понятий, развивается фантазия, уверенность в своих способностях, развивается чувство товарищества, взаимовыручки.

Игры можно применять на всех ступенях обучения, но совершенно необходимо – в работе младшего и среднего звена.

При использовании дидактических игр и игровых элементов следует придерживаться:

Определения места в системе других видов деятельности на уроке;
Целесообразность использования их на разных этапах изучения различного по характеру математического материала;
Разработка методики проведения дидактических игр с учетом дидактической цели урока и уровня подготовленности учащихся;
Требования к содержанию игровой деятельности в свете идей развивающего обучения.

Дидактические игры хороши в системе с другими формами обучения, использование, которых должно в конечном итоге привести к решению следующих задач:

учитель должен дать учащимся знания, которые соответствуют современному уровню развития науки;
научить учащихся самостоятельно приобретать знания.

Требования к организации дидактических игр:

игра должна основываться на свободном творчестве и самостоятельной деятельности учащихся;
игра должна быть доступной для данного возраста, цель игры - достижимой, а оформление красочным и разнообразным;
обязательный элемент игры – ее эмоциональность. Игра должна вызывать удовольствие, веселое настроение, удовлетворение от удачного ответа;
присутствие элемента соревнования между командами или отдельными участниками;
роль активности учащихся во время проведения игры;
воспитательное, познавательное значение игры.

Роль учителя при организации дидактических игр и игровых элементов:

положить начало творческой работе учащихся;
контроль и руководство учителя не должны подавлять инициативу и самостоятельность детей;
подготовить учащихся старшего возраста для проведения игр в 5 классе;
подготовить контрольные карты

Игры могут быть предметом специальных занятий в кружках, математических вечерах, предметных неделях. Классифицируя математические игры в зависимости от игровой цели, можно выделить 3 типа игр:

творческие игры;
игры с раздаточным материалом;
игры - соревнования.

Привожу некоторые примеры использования дидактических игр на уроках математики в 5-6 классах.

Игра «Соревнование художников»

На доске записаны координаты точек: (0;0),(-1;1),(-3;1),(-2;3),(-3;3),(-4;6),(0;8),(2;5),(2;11),(6;10),(3;9),(4;5),(3;0),(2;0),(1;-7),(3;-8),(0;-8),(0;0).

Отметить на координатной плоскости каждую точку и соединить с предыдущей отрезком. Результат – определенный рисунок.

Эту игру можно провести с обратным заданием: нарисовать самим любой рисунок, имеющий конфигурацию ломаной и записать координаты вершин.

Эта игра очень нравится учащимся.

Игра «Морской бой»

Эти игры развивают внимание, наблюдательность, сообразительность, ученики быстрее усваивают и убеждаются, что положение точки на плоскости определяется с помощью двух её координат.

Игра «Математическое лото»

Каждому ученику выдается конверт, в котором 1 большая карта с заданиями и маленькие, их больше, чем заданий. На маленьких – результаты вычислений. Ученик должен выполнить задание на большой карте и накрыть его ответом (результатом его вычислений). После выполнения всех заданий ученик переворачивает маленькие карточки и получает задание (если верно выполнены все вычисления). Например: определение целых чисел, правило сравнения, правило сложения, вычисление, деление, умножения целых чисел и др. Затем ученики выполняют полученные задания.

Игра «Магические квадраты»

А) В клетки квадрата записать такие числа, чтобы сумма чисел по любой вертикали, горизонтали была равна 0.

Б) Записать в клетки квадрата числа -1; 2; -3; -4; 5; -6; -7; 8; -9 так, чтобы произведение по любой диагонали, вертикали, горизонтали было равно положительному числу.

Игра «Забег по кругу»

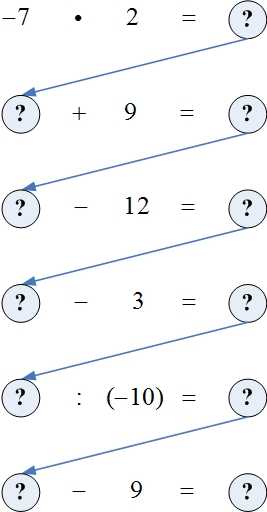
На доске записана цепочка примеров, которые нужно выполнить строго по указанию стрелки. При правильном выполнении заданий получают первое число цепочки.

Эти игры помогают усвоить все действия с целыми числами, вычислительные навыки, сообразительность, внимательность.

Игра «Цветочек»

В листе цветка помещается дробь, которую нужно сложить, умножить, разделить, вычесть. Дроби, с которыми нужно произвести эти действия, записаны на лепестках цветка.

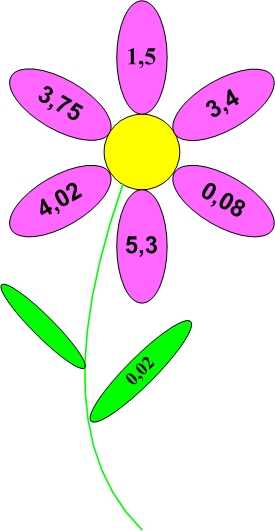
1) 1,5 ∙ 0,2

2) 3,75 ∙ 0,2

3) 3,4 : 0,2

4) 0,08 + 0,2

5) 4,02 + 0,2

6) 5,3 – 0,2

После того, когда ученики выполнят указанные действия, рисует на доске такой же цветок тот, кто первым выполняет все вычисления, только в лепестках пишет результаты вычислений.

Игра «Лучший счетчик»

Класс делится на три команды. Каждая выбирает «счетчика», который будет защищать свою команду. Примеры «счетчику» задают члены других команд до тех пор, пока он не собьется. Затем его сменяет «счетчик» другой команды. За каждый правильный ответ 1 очко. Побеждает команда, которая набрала больше очков. Условие игры – отвечать на вопросы быстро.

Игра «Индивидуальное лото»

28,53+1,47 (Р)

4,4+3,5 (О)

(3,2 - 0,2)+6 (Я)

0,5+8-4,6 (Д)

61,3 - х, если х=8 (К)

4 + 1,25 (А)

53,5 - 5 (З)

4,55+6+0,7 (Р)

11,25 (Р)

48,5 (З)

5,25 (А)

ольшая карта

30 (Р)

9 (Я)

3,9 (Д)

Интеллектуальный марафон (математика, 5 класс)

1. Если буквы слова "кенгуру" расположить в алфавитном порядке, какая буква окажется на третьем месте?

1) К

2) Е

3) Н

4) Г

5) Р

2. Сутки на планете Тамагочи на 40 минут длиннее, чем на планете Земля. На сколько неделя на Тамагочи отличается от недели на Земле?

1) 4 ч 40 мин

2) 2 ч 20 мин

3) 7 ч 20 мин

4) 40 мин

5) 28 ч

3. Решите анаграммы:

1) чадаза

2) гурк

3) чул

4) мапряя

5) резоток

4. Расшифруйте "закодированные" слова:

1) и100рия

2) про100р

3) кис.

4) 3тон

5) о3цание

5. Вычислите площадь квадрата, периметр которого равен 36 см2

1) 12 см2

2) 18 см2

3) 81 см2

4) 36 см2

5) 25 см2

6. Выберите самое маленькое четырехзначное число, в записи которого все цифры разные.

1) 1023

2) 1234

3) 1203

4) 1032

5) 1203

7. Корень уравнения х – 12678 = 25349 равен

1) 35428

2) 12675

3) 38027

4) 2671

5) 28027

8. Найдите значение выражения CXXV – XXXV

1) CX

2) CXI

3) IC

4) IICV

5) XC

Индивидуальное лото

Тема: «Десятичные дроби»

Цель: закрепить знания учащихся на действия с десятичными дробями.

Организация урока. В игре участвует весь класс или подгруппа

Описание игры: в специальном конверте учащимся предлагается набор карточек. Обычно их больше, чем ответов на контрольной карте, которая тоже вложена в конверт. Например, на большой карте нарисовано 6 прямоугольников, а у ученика 7 -8 карточек таких же размеров с записанными на них упражнениями. Ученик достает из конверта карточку, решает пример и накрывает ею соответствующий ответ. Карточки накладываются лицевой стороной вниз. Если все примеры решены, верно, то обратные стороны наложенных карточек составят слово, рисунок, букву. Учитель, проходя по рядам, легко определяет результаты работы.

Примеры карточек.

0,5 · 3,46 ׃ 2

0,5 · 5,6 · 5

34,47 · 0,9 + 5,53 · 0,9

4 · 1,75

28,53 · 0,8 +1,47

2,8 · 1,5 – 0,1

13,56х – 2,86х,

если х=0,4

7,86х + 2,14х,

если х=0,02

13,56х + 6,44х,

если х=0,6

22,4

Лучший счетчик

Темы: сложение и вычитание десятичных дробей, умножение и деление дробей.

Описание игры. Учитель объявляет, что на следующем занятии будет проходить игра под названием «Лучший счетчик». Дома каждый ученик должен подобрать по теме три четыре примера для устного счета. Класс делится на три команды. В каждой команде выбирается «счетчик», который будет защищать честь команды. Примеры для устного счета предлагают «счетчику» члены других команд до тех пор, пока он не собьется. Затем его сменяет другой ученик из той же команды, и игра продолжается.

Число «счетчиков» для одного тура определяется по договоренности.

Побеждает команда, в которой было наименьшее число «счетчиков», решивших наибольшее количество примеров. Среди «счетчиков» устанавливается личное первенство.

По аналогии можно провести игру: «Слабое звено» на закрепления темы: «Чтение и запись десятичных дробей». В данном случае учитель предлагает сам или «консультанты» карточки с записью дробей в письменном виде или словесном. Учащимся предлагается сидя за партами образовать «змейку» всех рядов или по рядам. Игра продолжается до тех пор, пока не определится разрыв «змейки». Так определяется «слабое звено» в «змейке». Учащимся, которые разорвали «змейку» предлагаются дополнительные задания.

Карточки заранее готовятся учителем или учащимися дома, затем они смешиваются и даются учащимся для выполнения. ( Опыт составителей)

Такие задания даются в начале урока и служат своеобразной разминкой для дальнейшей работы.

20. Написать какую – нибудь обыкновенную дробь, показать её числитель и знаменатель. Что они обозначают?

30. Какое число больше: 5/12 или 5/6? Доказать правильность своего ответа, используя рис.1.

40. Самое крупное животное на земле – синий кит, длина которого достигает 30м. Длина кашалота составляет лишь половину, а длина горбатого кита – 8/15 длины синего кита. Какой длины бывает кит – кашалот и горбатый кит?

( задания выдается на красной карточке).

50. п/у Пирожные уложены в коробки по 10 штук. Продано 3% коробки. Сколько штук пирожных продано?

60. Какая часть сентября прошла до сегодняшнего дня? Какая часть осталась?

20. Выразить в метрах: 3км80м, 128см,4см (выдается на красной карточке).

30. Сколько метров в километре, дециметре, сантиметре, декаметре, миллиметре? (выдается красная карточка).

40п/у. Выразить в сантиметрах и миллиметрах сумму: 6см5см + 3см7мм

50п/у. Вычислить:32дм – 20см

60 п/у. Длина отрезка 1м3дм5мм. Выразить её в миллиметрах, потом в метрах.

20. Как произошло слово дробь?

30. Что представляет собой эталон метра и где он хранится?

40. Иногда о ком говорят: «Косая сажень в плечах» Как это понимать?

50. Поехал крестьянин с дочкой в город на ярмарку. Накупил он ей подарков разных: ленты яркие кружева тонкие, бусы блестящие, румяна алые и взял ещё 2 локтя ситца пестрого. Можно ли из этого ситца платье сшить?

Математическое лото

Эта форма работы проводится при повторении изученного материала.

Описание: в коробку, мешок помещают шарики (свернутые в трубочку бумажки, картонные карточки) с номерами тех пунктов учебника, которые повторяют.

Класс делится на группы (по рядам: мальчики – девочки).

Команды составляют по 4 – 5 вопросов по каждому пункту. Учитель или помощник просит достать из коробки шарик показывает номер пункта. Соперники поочередно задают друг другу вопросы. Вопрос оценивается от 1 – 3 балла. Затем подсчитывается сумма баллов у каждой группы и определяется победитель.

Математический лабиринт

Лабиринт – греческое слово, означает ход в подземелье. Лабиринт – запутанная сеть дорожек, ходов, сообщающихся друг с другом помещений.

Найдите выход из запутанного положения: последняя цифра ответа решенного примера дает начало следующего.

Может найти применение:

При обработки вычислительных навыков, при закреплении и проверки изученного материала, а также при проведении самостоятельной работы практически любой темы за курс 5 – 6 классов.

Рассмотрим данную игру на примере устного счета.

1) 36*34=1224

2) 42*101=4242

3) 295*999=294705

4) 58*11=638

5) 87*93=8091

6) 17*99=1683

7) 69*101=6969

8) 99*93=9207

9) 764*25=19100

10) 33*82=2706

Таким образом, выстраивается последовательность решенных примеров

1 – 4 – 8 – 7 – 9 – 10 – 6 – 3 – 5 – 1 или

4 – 8 – 7 – 9 – 10 – 6 – 3 – 5 – 1 – 4 или

8 – 7 – 9 – 10 – 6 – 3 – 5 – 1 – 4 – 8 и так далее.

Учащимся можно одновременно предложить до 10 вариантов самостоятельной работы. Учителю очень легко осуществить проверку на глазах учеников (примеры даются без ответов).

Викторина

Это занимательный элемент на уроке когда остается время или если дети выполнили план урока.

На какое число надо разделить 8, чтобы получить 2
Когда делимое и частное, равны между собой?
Все числа 2,5; 2,6; 2,7; 2,8; 2,9; 3,1; 3,2; 3,3; 3,4 обладают одной особенностью, связанной с округление чисел. Какую?
Одного человека спросили: «Сколько вам лет?» «Порядочно, - ответил он». – «Я старше некоторых своих родственников в 600 раз». Возможно ли это? (Да, если родственник - младенец. Пусть, например ему 0,1 года, то есть 1,2 месяца, тогда 0,1.•600=60лет, что вполне допустимо.)
Разделить 5 яблок между пятью лицами так, чтобы каждый получил по яблоку и одно яблоко, осталось в корзине. (Один берет яблоко с корзиной)
Сколько будет трижды сорок и пять?
В комнате четыре угла. В каждом углу сидит кошка. Напротив каждой кошки по три кошки. На хвосте каждой кошки по оной кошке. Сколько же всего кошек в комнате?(4 кошки)
Когда делимое и частное будут равны?

Логическая задача

Такие задачи можно включать при изучении тем: по статистики и теории вероятностей

Подготовка: заранее вывешивается таблица

Задача. В кругу сидят Иванов, Петров, Карпов, и Марков. Их имена: Андрей, Сергей, Тимофей, и не Андрей;

Иванов не Алексей и не Андрей;

Сергей сидит между Марковым и Андреем;
Карпов не Сергей и не Алексей;
Петров сидит между Карповым и Андреем.

Кто есть кто?

Таблица.

Иванов

Петров

Марков

Карпов

Иванов

Петров

Марков

Карпов

Логический практикум

Комментируя какую – нибудь самостоятельную работу или контрольную, учитель говорит ученику: «Не уверен друг мой, что эта оценка окажется для тебя неприятной» Затем предлагается ученику выбрать из пяти вариантов ответ, который он имел ввиду:

Уверен, что эта оценка будет тебе приятной.
Уверен, что эта оценка будет тебе неприятна.
Уверен, что эта оценка не будет тебе приятной.
Похоже, что эта оценка будет тебе приятной.
Похоже, что эта оценка будет тебе неприятна?

Игра «Счастливый случай» 6 класс.

Цель: формирование интереса к математике, развитие кругозора.

Задачи: Развивать внимание, тренировать память, учить учащихся быстро думать и принимать правильное решение, воспитывать чувство взаимовыручки.

1 гейм

Вопросы каждой команде задаются по очереди.

1. Как найти неизвестное делимое? Как найти неизвестный делитель?

2. Бежала тройка лошадей. Каждая лошадь пробежала 5км. Сколько проехал ямщик? (5км.)

Шла старуха в Москву. Навстречу ей 3 старика. Сколько человек шло в Москву? (1 старуха).

З.Чему равна 1/4 часть часа? (15мин.)

Какую часть часа составляют 20минут? (1/3).

4. Как называют 1 кубометр воды? (тонна)

Как называют объем 1кг воды? (литр)

2 гейм

Кто вперед из команд ответит на вопрос?

1 .Чему равен угол в квадрате? (90)

2.Единица измерения скорости на море (узел)

З.Что легче: 1кг ваты или 1кг железа? (одинаково) 4.Число разрядов в классе (три)

5.Найти 1 процент рубля (1 коп)

6.Прибор для построения окружностей (циркуль)

7.К натуральному числу справа приписали три нуля. Во сколько раз увеличилось число? (в 1000)

8.Как называется первая координата точки на плоскости? (абсцисса)

9.Наименьшее натуральное число. (1) 10.Наименьшее простое число. (2)

3 гейм Ты мне - я тебе

Ученики готовят дома заранее вопрос и ответ.

4 гейм

Темная лошадка.

Вытягивают номера вопросов из мешка. Номер 7 - счастливый случай.

1 .Дайте определение понятию «процент».

2.К однозначному числу, большему нуля, приписали такую же цифру. Во

сколько раз увеличилось число? (в 11)

3.Число, обращающее уравнение в верное числовое равенство (корень

уравнения).

4.Отрезок, соединяющий точку окружности с центром ( радиус)

5.Площадь прямоугольника 36 кв.см. Чему равна сторона квадрата с такой же площадью? (6см).

6.Разделите сто на половину.(200).

7. Счастливый случай.

8.Формула площади прямоугольника со сторонами х и у.

5 гейм. Дальше - дальше.

За одну минуту надо дать как можно больше правильных ответов.

1 .Первая буква греческого алфавита (альфа)

2.Может ли при умножении получиться ноль? (да)

З.Чему равно 13*25*0*0,7? (0).

4.Единица массы драгоценных камней (карат).

5.Прибор для измерения углов (транспортир).

6.Чему равна сумма углов квадрата? (360).

7.Как называется вторая координата точки на плоскости? (ордината).

8.Чему равна длина окружности?

9.В чем измеряются углы? (в градусах).

10.Равенство, содержащее букву (уравнение).

11.9*8=? (72).

12.Чему равен 1 пуд? (16кг).

13.Одно яйцо вкрутую варится 5 минут, а 5 яиц? (5мин)

14.0,25* 100=? (25).

15.Как называются отрезки, которые никогда не пересекаются? (параллельные).

16.Каким действием находится дробь от числа? (умножением).

17.Может ли при делении получиться ноль? (да).

18.Дано 8. Найти ему противоположное (-8).

19.Назвать число, обратное 12.(1/12)

20.Что такое разность чисел? (результат вычитания).

21.Назвать самое меньшее число, кратное 7.(7).

22 .Как называются прямые, пересекающиеся под углом 90 градусов? (перпендикулярные).

23 .Что такое пропорция? (равенство двух отношений.)

24.Что называют подобными слагаемыми? (Слагаемые, имеющие одинаковую

буквенную часть.)

25.Сколько граней у куба? (6)

26.Сколько сторон у треугольника? (три).

27.Чему равен развернутый угол? (180).

28.Чему равна сумма углов треугольника? (180).

29.Как называют число, которое складывают? (слагаемое).

30.Луч, который делит угол пополам (биссектриса).

Подведение итогов. Слово жюри.

Игра «Кто хочет стать отличником?»

Порядок игры:

1.Отбор игроков среди присутствующих.

Условия игры:

После ответа на 5-й вопрос игрок получает первую пятерку (несгораемую).

После ответа на 10-й вопрос получает вторую пятерку (несгораемую).

После ответа на 15-й вопрос получает третью пятерку и звание отличника.

Ведущий читает вопросы и варианты ответов по вопроснику, а игрок имеет возможность видеть эти вопросы и варианты ответов на экране.

Если игрок ошибся, то он выбывает из игры, заработав или не заработав пятерки, а оставшиеся вопросы можно задавать зрителям. За каждый правильный ответ можно давать жетоны. Кто наберет больше жетонов, тот участвует в следующей игре.

Вариант 1.

1. Как называется учебное время между каникулами?

А. Тайм; В. Четверть; С. Семестр; Д. Период.

2. Сколько длится большая перемена?

А. 15 минут; В. 20 минут; С. 10 минут; Д. 25 минут.

3. Сколько часов в сутках?

А. 25 часов; В. 23 часа; С. 26 часов; Д. 24 часа.

4. Сколько дней в феврале?

А. 28; В.30; С. 31; Д. 33.

5. Как называется 11-й месяц?

А. Декабрь; В. Ноябрь; С. Октябрь; Д. Январь.

6. В 1 т:

А. 100 кг; В. 1000 кг; С. 10 кг; Д. 10 000 кг.

7. Сумма – это результат:

А. Умножения чисел; В. Деления чисел; С. Сложения чисел; Д. Вычитания чисел.

8. 524 – это:

А. 5 сотен 2 единицы 4 десятка; В. 5 сотен 2 десятка 4 единицы;

С. 5 десятков 2 сотни 4 единицы; Д. 5 единиц 2 сотни 4 десятка.

9. Сколько будет 256х0?

А. 256; В. 2560; С. 0; Д. 2056.

10. У квадрата:

А. Все стороны разные; В. Противоположные стороны равны;

С. Все стороны равны; Д. Три стороны равны.

11. Сколько будет 7х8?

А. 72; В. 63; С. 64; Д. 56.

12. На сколько 20 больше 4?

А. на 24; В. На 16; С. На 5; Д. на 80.

13. У равностороннего треугольника:

А. Все стороны равны; В. Все стороны разные; С. Есть прямой угол; Д. Все стороны равны.

14. В прямоугольном треугольнике:

А. Все углы прямые; В. Два угла прямые; С. Один угол прямой; Д. Все стороны равны.

15. Произведением каких чисел можно представить число 42?

А. 6и6; В. 4и10; С. 7и 6; Д. 7и 7.

Вариант 2.

1. Как называется промежуток времени между четвертями?

А. Перемена; В. Отпуск; С. Пересменка; Д. Каникулы.

2. Сколько минут идет урок?

А. 45 минут; В. 50 минут; С. 40 минут; Д. 35 минут.

3. Сколько дней в неделе?

А. 6 дней; В. 8 дней; С.5 дней; Д. 7 дней.

4. Сколько лет в веке?

А. 10; В.100; С. 200; Д. 1 000.

5. Как называется 4-й месяц?

А. Май; В. Апрель; С. Июнь; Д. Март.

6. В 1цт:

А. 10 кг; В. 1000 кг; С. 100 кг; Д. 10 000 кг.

7. Разность – это результат:

А. Умножения чисел; В. Деления чисел; С. Сложения чисел; Д. Вычитания чисел.

8. 732 – это:

А. 7 сотен 3 единицы 2 десятка; В. 7 сотен 3 десятка 2 единицы;

С. 7 десятков 3 сотни 2 единицы; Д. 7 единиц 3 сотни 2 десятка.

9. Сколько будет 24х1?

А. 241; В. 24; С.23; Д. 124.

10. Луч – это часть прямой, ограниченная:

А. С двух сторон; В. С одной стороны;

С. С трех сторон; Д. С четырех сторон.

11. Сколько будет 7х9?

А. 64; В. 56; С. 63; Д. 72.

12. Во сколько раз 20 больше 4?

А. в 16 раз; В. В 5 раз; С. В 24 раза; Д. в 80 раз.

13. В остроугольном треугольнике:

А. Два угла острые; В. Один угол прямой; С. Есть тупой угол; Д. Все углы острые.

14. . В треугольнике могут быть:

А. Два тупых угла; В. Четыре тупых угла; С. Три тупых угла; Д. Один тупой угол.

15. Суммой каких чисел можно представить число 35?

А. 10 и 15; В. 24 и 5; С. 15 и 20; Д. 14 и 7.

Сказочная математика

ВАРИАНТ № 1.

1. Собралась Баба Яга на шабаш. Чем удивить подружек? Решила Баба Яга испечь громадный пирог с лягушками. Открыла кулинарную книгу и прочитала, что на приготовление маленького пирожка с лягушками (всего 1,5 кг) требуется 33 лягушки. Стала Баба Яга считать, сколько же лягушек заказать кикиморам, чтобы испечь громадный пирог весом 35 кг, да так до сих пор и считает. Помоги Бабе Яге: посчитай, сколько лягушек потребуется на такой пирог.

2. Не хотела Василиса Прекрасная выходить замуж и задала глупым своим женихам "неразрешимую" задачу: "15 раз по 15 синиц смогут очистить мой лес от гусениц за 15 лет. Сколько лет потребуется 3 раза по 3 синицам, чтобы проделать ту же работу?" А ты сможешь решить эту задачу?

ВАРИАНТ № 2.

1. Имел Царь Василий Пупкин громадное царство, и было в нем 7 лесов и 7 морей. Полжизни воевал Василий, чтобы увеличить свои богатства, и удалось ему расширить свои владения: теперь у него уже 33 леса и 33 моря. Задумался царь, какую же стражу теперь ему требуется содержать, чтобы охранять все это и поддерживать порядок в царстве? Призвал своих мудрецов (а в их числе и ты) и велел посчитать количество стражи: если раньше ему хватало 119 тысяч стражников, то сколько требуется теперь?

2. Спорят Леший с Кикиморой: -Чьё болото? - и пришли за разрешением спора к Бабе Яге, а Баба Яга задала им задачу - кто правильно ответит, тот и владелец болота: "Ваше болото Водяной выпьет за 77 дней, а змей Горыныч имеет голов в 7 раз больше, чем Водяной, да каждая из них пьет в 33 раза медленней. Сколько дней Змею Горынычу пить ваше болото?" Что им отвечать?

ВАРИАНТ № 3.

Ужинали вместе Змей Горыныч и Кощей Бессмертный и решали давний спор: кому свататься к Бабе Яге? Спорили они спорили и решили, что свататься будет тот, кто умнее, и решит задачу другого. Решите эти задачи:

1. Змей Горыныч - Кощею Бессмертному: "Лететь мне от своего царства до Бабы Яги 3 дня и 3 ночи, а расстояние между нами 33 раза по 33 версты. Сколько же мне лететь от своего царства до тебя, если между нами все полные 3993 версты?"

2.Кощей Бессмертный - Змею Горынычу: "Богат я, Змей Горыныч, да нет у меня кареты, чтобы ехать свататься, а мастер просит за карету 144 золотых перстня по 144 унции каждый. Перстни у меня есть, да только мне проще отдать цепями. Сколько же мне нужно отдать цепей, если каждая весит 324 унции?"

ВАРИАНТ № 4.

1. Расчесывает Василиса Прекрасная свои чудесные кудри и считает: "Живу я в этом новом замке уже 25 раз по 25 дней и успела обломать о свои кудри 44 гребня. Сколько же гребней мне заказывать золотому мастеру на следующие 5000 дней?"

2. Решает Водяной вопрос об охране болота, так как многие старые жабы просятся на покой и подросли молодые лягушата. Каждая старая жаба квакает 24 раза в день, и каждый ее квак длится по 2/3 глухариной песни. Молодые лягушата квакают чаще - 33 раза в день, да каждый их квак длится всего 0,1 глухариной песни. Сколько молодых лягушат призвать на действительную службу, чтобы болото охранялось так же оглушительно, если на пенсию подали заявление 33 старых жабы?

В ходе игры вырабатывается быстрота вычислений, внимательность, сообразительность.

Основным в дидактической игре на уроках математики является обучение математике. Игровые ситуации лишь активизируют деятельность учащихся, делают восприятие более активным, эмоциональным, творческим. Создание игровых ситуаций на уроках повышает интерес к предмету, вносит разнообразие и эмоциональную окраску в учебной работе, снижает утомление, развивает внимание, взаимопомощь.

Дидактические игры влияют на повышение качества знаний, умений и навыков учащихся, развитие умственной деятельности.

infourok.ru

Дидактические игры на уроках математики

Разделы: Начальная школа

«Живой уголок»

Дидактическая цель: ознакомление детей с приемом образования чисел при одновременном закреплении пространственной ориентации, понятий «больше», «меньше».

Средства обучения: изучение животных.

Содержание игры: учитель говорит: «В нашем живом уголке живут кролики: серый и белый, кролики грызут морковь. Сколько кроликов грызут морковь? (два, ответ фиксируется показом цифры 2). Назовите, какие кролики грызут морковь? (серый и белый). К ним прибежал еще один кролик. Что изменилось? (кроликов стало больше) Сколько кроликов теперь едят морковь? (три, ответ фиксируется показом цифры 3) Перечисли их (один белый и еще один белый, и еще один серый, всего три). Каких кроликов больше, белых или серых? (белых) Почему их больше? (их два, а два это один и один). Почему 2>1? (два идет при счете после числа 1). Аналогично можно рассматривать образование последующих чисел.

«Лучший счетчик»

Содержание игры: учитель на магнитном моделеграфе по секторам соответственно размещает от 1 до 10 рисунков. Открывая каждый сектор поочередно, учитель предлагает детям сосчитать число рисунков и показать нужную цифру. Сосчитавший первый называется лучшим счетчиком. Затем учитель показывает цифры вразбивку, а ученики – соответствующее число рисунков в секторах круга. В итоге игры учитель открывает 2 сектора, предлагает сравнить число рисунков в них и определить, где предметов меньше и на сколько.

«Хлопки»

Содержание игры: учитель на магнитном моделеграфе размещает по секторам от 1 до 10 рисунков. Открывая по очереди сектор за сектором, предлагает сосчитать число рисунков и по его сигналу похлопать столько же раз, сколько открыто рисунков, и показать нужную цифру. (Учитель задает ритм хлопков).

«Числа, бегущие навстречу друг другу»

Дидактическая цель: знакомство с составом числа 10.

Содержание игры: учитель предлагает детям записать в тетради числа от 1 до 10 по порядку и дугами показать два числа, которые бегут навстречу друг другу, образуя в сумме число 10. Затем просит записать примеры на сложение с этими числами.

Например:

0 1 2 3 4 5 6 7 8 9 10

0 +10 = 10 - 10 + 0 = 10

1 + 9 = 10 - 9 + 1 = 10

«Математическая эстафета»

Дидактическая цель: ознакомление с образованием чисел из десятка и единиц.

Средства обучения: 10 кругов и 10 треугольников из приложенных к учебнику математики для 1 класса.

Содержание игры: учитель делит класс на 3 команды по рядам и проводит игру-соревнование. Первый ученик из первой команды иллюстрирует число с помощью кругов и треугольников, второй из этой же команды называет обозначенной число, третий – его состав, четвертый показывает число на карточках.

Аналогичные упражнения выполняют из второй и третий команд. Победит та команда, которая не допустит ни одной ошибки или допустит меньшее их число.

При изучении нумерации чисел в пределах 100 задача состоит в том, чтобы научить считать и записывать числа. Установлению связи между устной и письменной нумерацией поможет известная игра «Молчанка».

Содержание игры: учитель иллюстрирует на абаке или карточках двузначные числа, а учащиеся обозначают их с помощью разрезных цифр и показывают их молча учителю или записывают в тетради.

«Как запутался Сережа?»

Сережа научился писать числа в пределах сотни. Однажды вечером отец положил перед Сережей на стол 4 палочки слева и один десяток связанных палочек справа и предложил мальчику написать, сколько палочек всего. Сережа написал число 41. Правильно ли написал число Сережа? Как он рассуждал?

«Подарки Петрушки»

Дидактическая цель: ознакомить с составом числа 5.

Средства обучения: иллюстрации Петрушки, Незнайки и Веселого Карандаша; воздушные шары, вырезанные из цветного картона.

Содержание игры: учитель сообщает, что на урок в гости пришел Петрушка с воздушными шарами и с ним пришли его друзья. Незнайка и Веселый Карандаш (на доску крепятся иллюстрации с изображением сказочных героев). Петрушка решил подарить шары Незнайке и Веселому Карандашу. Как он может подарить их?

Дети перечисляют возможные варианты состава числа пять и иллюстрируют у доски и после записывают в тетрадь. В конце игры наиболее активные дети поощряются.

«Украсим елку игрушками»

Дидактическая цель: знакомство с составом числа 10.

Средства обучения: рисунок елки; маленькие иллюстрации елочек для учащихся.

Содержание игры: учитель сообщает, что скоро Новый год. И все будут наряжать елку. И нам с вами тоже надо нарядить елку. Наша елка – математическая. На доску вывешивается плакат с елкой. На верхушке – звезда с числом 10. Но не все ветки украшены игрушками, надо повесить еще недостающие шарики так, чтобы на каждом ярусе сумма чисел была равна 10. Дети выходят к доске и наряжают елку. Учитель должен поощрять слабых детей.

«Цепочка»

Содержание игры: учитель выставляет для каждого ряда (команды) на подставку доски карточки, изображающие числа вида:

Выигрывает команда, которая допустит меньше ошибок в образовании двузначных чисел. Для подведения итогов игры учитель отмечает в таблице звездочками правильные ответы учащихся.

«Контролеры»

Дидактическая цель: закрепление знания состава чисел первого десятка.

Содержание игры: учитель распределяет детей на две команды. Два контролера у доски следят за правильность ответов: один – первой команды, второй - другой команды. По сигналу учителя ученики первой команды делают несколько ритмических наклонов вправо, влево и считают про себя. По сигналу учителя они называют хором число наклонов первой команды до заданного числа и ведут счет про себя (например, 6 – прибавил, 1,7 – прибавил 2,8 – прибавил 3). Затем они называют число выполненных наклонов. По числу наклонов, выполненных учениками 1 и 2 группы, и называется состав числа. Учитель говорит: «Восемь – это…», ученики продолжают: «Пять и четыре». Контролеры показывают зеленые круги в правой руке, если согласны с ответом, красный - если нет. В случае ошибки упражнение повторяется. Потом учитель предлагает детям второй команды по сигналу делают несколько приседаний, а ученики первой команды дополняют приседания до заданного числа. Называется состав числа. Аналогично анализируется состав чисел на основе хлопков.

Сколько палочек в другой руке?

Дидактическая цель: закрепление знания десятичного состава двузначного чисел.

Средства обучения: набор отдельных палочек и пучков палочек.

Содержание игры: вызванный ученик берет пучок палочек в одну руку, а отдельные палочки – в другую руку и показывает их классу. Дети угадывают их количество и показывают карточку с соответствующим числом.

«Хлопки»

Цель игры: закрепления знания десятичного состава двузначного чисел.

Средства обучения: набор определенных палочек и пучков палочек.

Содержание игры: учитель вызывает двух детей к доске. Ученик, стоящий справа, обозначает единицы, а стоящие справа – десятки. Учитель называет двузначное число, правый ученик хлопками обозначает число единиц в этом числе, а левый – число десятков. Все остальные ученики выполняют роль контролеров. Они сигналят, если десятичный состав числа показан учениками неверно.

«Стук-стук»

Дидактическая цель: закрепление знания по нумерации чисел в пределах 20.

Средства обучения: на доске изображена таблица с двумя разрядами:

Десятки	Единицы

Содержание игры: учитель молча стучит указкой один раз в разряде десятков и несколько раз в разряде единиц. Дети внимательно слушают и показывают учителю соответствующее число на карточке с цифрами.

Для закрепления навыков счета можно предложить игру «Слушай и считай»:

Содержание игры: у каждого из учеников набор карточек с числами от 1 до 10. У учителя палочка, которой он ударяет по какому-либо предмету, издающему громкий звук, определенное число раз. Все учащиеся должны немедленно поднять и показать карточку с числом, соответствующим количеству ударов.

Можно условиться, что играющие, услышав удары, должны поднять карточку с числом, недостающим, например, до десяти (ударов было три, поднять карточку с числом 7). Затем устанавливается другое правило: показать надо не число, соответствующее числу ударов, а два соседних числа – меньшее и большее. Можно предложить и другой вариант игр: учитель сначала ударит палочкой по одному предмету 8 раз, а по другому – 3 раза. Это значит, что учащиеся должны от восьми отнять три и показать карточку с числом 5. Игра требует тишины и внимания, поэтому можно предложить ребятам, прислушиваясь к числу ударов, закрывать глаза.

«Назови соседей числа»

Эта игра дает возможность каждое число первой сотни рассматривать не изолированно, а в связи с предыдущим и последующим числом.

Средства обучения: мяч или два мяча – большой и маленький (или разного цвета).

Содержание игры: учитель бросает мяч то одному, тот другому участнику игры, а те, возвращая мяч, отвечают на вопрос учителя. Бросая мяч, учитель называет какое-либо число, например двадцать один, играющий должен назвать смежные числа –20 и 22 (обязательно сначала меньшее, потом большее).

«Кто быстрей сосчитает?»

Игра развивает зоркость, внимание.

Содержание игры: на доске вывешиваются два одинаковых плаката, на которых записаны в произвольном порядке числа. Например, от 61 до 90 (от 11 до 30 и т.п.). Например, требуется назвать и указать на таблице по порядку все числа от 61 до 90. Можно соревноваться и двумя командами, по одному человеку от каждой. Затем победители соревнуются между собой и определяется лучший счетчик.

Примерный вид плаката:

90	75	71	63	66
67	82	86	68	76
87	61	73	89	81
74	88	65	77	84
80	69	78	62	70
64	83	72	79	85

Также на этапе закрепления можно предложить следующие игры:

«Загадка»

Дидактическая цель: закрепить нумерацию чисел в пределах 100; десятичный состав числа.

Содержание игры: учитель загадывает загадку «Серебристая пила в небе ниточку вила. Кто же смелый нитью белой небо шил, да поспешил: хвост у нитки распушил?». Замени число десятками и единицами и в таблице найди буквы. Прочитайте слово и запишите его.

	5 ед.	6 ед.	7 ед.
3 дес.	К	Д	Ч
7 дес.	Т	Л	М
9 дес.	И	Ю	Ё

Ответ: летчик.

«Гном»

Дидактическая цель: закрепить умение детей заменять двузначное число суммой его разрядных слагаемых.

Содержание игры: Помоги гному найти дорогу к дому. Куда идти: вперед или назад – об этом числа говорят. Замени каждое число суммой разрядных слагаемых и в таблице найди букву. Составь слово, прочитай.

	4	5	7
80	В	Ё	П
50	Д	Р	М
20	О	О	Е

Ответ: вперед.

«По порядку номеров»

Дидактическая цель: закрепление порядка следования чисел при счете.

Содержание игры: две команды по 10 человек выстраиваются шеренгами лицом к классу. У ведущего – два комплекта карточек разного цвета с числами от 1 до 10 (можно использовать любые варианты чисел). Пред началом игры ведущий перемешивает карточки каждого комплекта и по одной прикрепляет на спины играющих. Ни один из играющих не знает, какое число на его карточке. Узнать это каждый может лишь у своего соседа. По сигналу игроки команд должны построится так, чтобы числа на их карточках были расположены по порядку. Команда, выполнившая задание быстрее и точнее, выигрывает.

«Сбежавшие числа»

Дидактическая цель: усвоение порядка следования чисел в натуральном ряду.

Материал игры: таблички числами.

«Рыболовы»

Дидактическая цель: анализ однозначных и двузначных чисел.

Содержание игры: на наборном полотне изображен пруд; в прорези полотна вставлены изображения рыбок, на которых написаны двузначные и однозначные числа. Соревнуются две команды по 4 человека в каждой. Поочередно каждый член команды «ловит рыбку» (громко называет число) и проводит его анализ: сколько знаков в числе, его место в числовом ряду, разбор чисел по десятичному составу. Если все ответы правильны, то он поймал рыбку (берет её), если нет – рыбка сорвалась. Выигрывает команда, поймавшая больше рыбок.

«Борьба за цифру»

Дидактическая цель: закрепление порядка следования чисел.

Средства обучения: два больших листа плотной бумаги, на которых написаны разным цветом цифры большого размера.

Содержание игры: перед каждой таблицей становится один из учеников. Учитель предлагает громко назвать числа по порядку от 1 до 24 и от 52 до 75, одновременно показывая каждое из них на таблице. Тот, кто быстрее назовет числа, считается победителем. Через каждую таблицу проходит несколько пар.

Пример таблицы:

14	8	12	4
10	23	1	15
3	17	21	7
19	6	9	11
24	2	16	22
13	20	5	18

65	59	63	55
61	74	52	66
54	68	72	58
70	57	60	62
75	53	67	73
64	71	56	69

С помощью этих игр в процессе обучения были не только закреплены знания учащихся, но и активизировано внимание учащихся. С помощью игры «Веселый счет» развивалось также и зрительное восприятие детей.

xn--i1abbnckbmcl9fb.xn--p1ai

Дидактические математические игры для дошкольников

План:

I Влияние игр на воспитание и развитие ребенка

II Дидактические игры на занятиях по математике

Игры с цифрами
Путешествия во времени
Игры на ориентацию в пространстве
Игры с использованием геометрических фигур
Игры на развитие логического мышления

III Значение игры

Дидактические математические игры для дошкольников

Лагойко Елена Михайловна,

воспитатель МБДОУ «ЦРР-д/с «Радуга», г. Абакан

“Без игры нет и не может быть полноценного умственного развития.

Игра – это огромное светлое окно, через которое в духовный мир ребенка вливается живительный поток представлений, понятий.

Игра – это искра, зажигающая огонек пытливости и любознательности.”

В.А. Сухомлинский.

«Палка, палка, огуречик – получился человечек» - именно так начинается знакомство малышей с... математикой.

Эта строчка песенки - переведенный на детский язык пример, иллюстрирующий: «Схема предмета состоит из следующих составляющих». Начиная развивать ребенка и знакомить его с миром математики, все мы наверняка хотим, чтобы малыш не просто «подготовился к школе», а действительно заинтересовался математикой и понимал эту науку. Чтобы достигнуть успеха на этом поприще, используя математические игры для дошкольников, важно учитывать следующее. Язык математики – это язык абстракции, логики и символа. Чтобы действительно понимать эту науку, впоследствии быть успешным в школе, научиться решать задачи, малышу прежде всего необходимо понять, а не заучить, о чем идет речь.

1. Важнейшее условие любого, не только математического занятия: оно должно оставаться игрой. В игре ребенок приобретает новые знания, умения, навыки. Игры, способствующие развитию восприятия, внимания, памяти, мышления, развитию творческих способностей, направлены на умственное развитие дошкольника в целом.

Работая в детском саду, я всегда ставлю перед собой такие педагогические задачи: развивать у детей память, внимание, мышление, воображение, так как без этих качеств немыслимо развитие ребенка в целом.

Используя различные дидактические игры, занимательные упражнения в своей работе, я смогу заполнить пробелы знаний у детей. “Влияние дидактических игр на развитие математических способностей у детей дошкольного возраста ”.

Все дидактические игры я для себя разделила на несколько групп:

Игры с цифрами и числами
Игры путешествие во времени
Игры на ориентировки в пространстве
Игры с геометрическими фигурами
Игры на логическое мышление

В настоящее время продолжаю обучение детей счету в прямом и обратном порядке, добиваюсь от детей правильного использования как количественных, так и порядковых числительных. Используя сказочный сюжет и дидактические игры, познакомила детей с образованием всех чисел в пределах 10, путем сравнивания равных и неравных групп предметов. Сравнивая две группы предметов, располагала их то на нижней, то на верхней полоске счетной линейки. Это я делала для того, чтобы у детей не возникало ошибочное представление о том, что большее число всегда находится на верхней полосе, а меньшее на - нижней.

Используя игры, учу детей преобразовывать равенство в неравенство и наоборот – неравенство в равенство. Играя в такие дидактические игры как Какой цифры не стало? Сколько? Путаница? Исправь ошибку, убираем цифры, назови соседей, дети научились свободно оперировать числами в пределах 10 и сопровождать словами свои действия.

Дидактические игры, такие как задумай число, составь цифру, кто первый назовет, которой игрушки не стало? И многие другие я использую на занятиях в свободное время, с целью развития у детей внимания, памяти, мышления.

Игра считай не ошибись! помогает усвоению порядка следования чисел натурального ряда, упражнения в прямом и обратном счете. В игре используется мяч. Дети встают полукругом. Перед началом игры говорю, в каком порядке (прямом или обратном) буду считать. Затем бросаю мяч и называю число. Тот, кто поймал мяч, продолжает считать дальше, Игра проходит в быстром темпе, задания повторяются многократно, чтобы дать возможность как можно большему количеству детей принять в ней участие. Такое разнообразие дидактических игр, упражнений, используемых на занятиях и в свободное время, помогает детям усвоить программный материал. Для подкрепления порядкового счета помогают таблицы, со сказочными героями, направляющимися к Вини - Пуху в гости. Кто будет первый? Кто идет второй и т.д.

2.В старшей группе познакомила детей с днями недели. Объяснила, что каждый день недели имеет свое название. Для того, чтобы дети лучше запоминали название дней недели, мы обозначали их кружочком разного цвета. Наблюдение проводим несколько недель, обозначая кружочками каждый день. Это я сделала специально для того, чтобы дети смогли самостоятельно сделать вывод, что последовательность дней недели неизменна. Рассказала детям о том, что в названии дней недели угадывается, какой день недели по счету: понедельник – первый день после окончания недели, вторник- второй день, среда – середина недели, четверг – четвертый день, пятница – пятый. После такой беседы я предлагала игры с целью закрепления названий дней недели и их последовательности. Дети с удовольствием играют в игру живая неделя. Для игры вызываю к доске 7 детей, пересчитываю их по порядку, даю им в руки кружочки разного цвета, обозначающие дни недели.Дети выстраиваются в такой последовательности, как по порядку идут дни недели. Например, первый ребенок с желтым кружочком в руках, обозначающий первый день недели – понедельник и т.д.

Затем, усложняла игру тем, что строились дети начиная с любого другого дня недели. Использовала разнообразные дидактические игры назови скорее, дни недели, назови пропущенное слово, круглый год, двенадцать, которые помогают детям быстро запомнить название дней недели и название месяцев, их последовательность.

3.Пространственные представления детей постоянно расширяются и закрепляются в процессе всех видов деятельности. Дети овладевают пространственными представлениями: слева, справа, вверху, внизу, впереди, сзади, далеко, близко.

Я поставила перед собой задачу научить детей ориентироваться в специально созданных пространственных ситуациях и определять свое место по заданному условию. Дети свободно выполняют задания типа: Встань так, чтобы справа от тебя был шкаф, а сзади – стул. Сядь так, чтобы впереди тебя сидела Таня, а сзади - Дима. При помощи дидактических игр и упражнений дети овладевают умением определять словом положение того или иного предмета по отношению к другому: Справа от куклы стоит заяц, слева от куклы – пирамида и т.д. В начале каждого занятия проводила игровую минутку: любую игрушку прятала где-то в комнате, а дети ее находили, или выбирала ребенка и прятала игрушку по отношению к нему (за спину, справа, слева и т.д.). Это вызывало интерес у детей и организовало их на занятие. Выполняя задания по ориентировке на листе бумаги, некоторые дети допускали ошибки, тогда я давала этим ребятам возможность самостоятельно найти их и исправить свои ошибки. Для того, чтобы заинтересовать детей, чтобы результат был лучше, предметные игры с появлением какого-либо сказочного героя. Например, игра найди игрушку, - “Ночью, когда в группе никого не было” – говорю детям, – “к нам прилетал Карлсон и принес в подарок игрушки. Карлсон любит шутить, поэтому он спрятал игрушки, а в письме написал, как их можно найти.” Распечатываю конверт читаю: “Надо встать перед столом воспитателя, и пройти 3 шага и т.д. ”. Дети выполняют задание, находят игрушку. Затем, когда дети хорошо стали ориентироваться, задания для них усложнила – т.е. в письме были не описание местонахождения игрушки, а только схема. По схеме дети должны определить, где находится спрятаный предмет. Существует множество игр, упражнений, способствующих развитию пространственных ориентировок у детей: найди похожую, расскажи про свой узор, мастерская ковров, художник, путешествие по комнате и многие другие игры. Играя с детьми я заметила, что они стали хорошо справляться со всеми заданиями, стали употреблять слова для обозначения положения предметов на листе бумаги на столе.

4.Для закрепления знаний о форме геометрических фигур с целью повторения материала средней группы, предлагала детям узнать в окружающих предметах форму круга, треугольника, квадрата.

Например спрашиваю: Какую геометрическую фигуру напоминает дно тарелки? (поверхность крышки стола, лист бумаги т.д.)

С целью закрепления знаний о геометрических фигурах. Проводила игру типа ЛОТО. Детям предлагала картинки (по 3-4 шт. на каждого), на которых они отыскивали фигуру, подобную той, которую я демонстрировала. Затем, предлагала детям назвать и рассказать, что они нашли. Занимаясь с детьми, я поняла, что дети, вновь пришедшие в детский сад плохо знают геометрические фигуры, поэтому с ними я занималась в основном индивидуально, давая детям сначала простые упражнения, а затем более сложные. Опираясь на полученные ранее знания познакомила детей с новым понятием четырехугольник. При этом использовала имеющиеся у дошкольников представления о квадрате. В дальнейшем, для закрепления знаний, в свободное от занятий время, детям давала задания нарисовать на бумаге разные четырехугольники, нарисовать четырехугольники, у которых все стороны равны, и сказать как они называются, сложить четырехугольник из двух равных треугольников и многое другое.

В своей работе использую множество дидактических игр и упражнений, различной степени сложности, в зависимости от индивидуальных способностей детей. Например, такие игры как найди такой же узор, каждую фигуру на свое место, подбери по форме. Чудесный мешочек, кто больше назовет.

Дидактическую игру геометрическая мозайка использую на занятиях и в свободное время, с целью закрепления знаний о геометрических фигурах, с целью развития внимания и воображения у детей.

Перед началом игры детей делю на две команды в соответствии с уровнем их умений и навыков. Командам даю задания разной сложности. Например:

а) Составление изображения предмета из геометрических фигур

б) Работа по условию (собрать фигуру человека, девочка в платье)

в) Работа по собственному замыслу (просто человека)

Каждая команда получает одинаковые наборы геометрических фигур. Дети самостоятельно договариваются о способах выполнения задания, о порядке работы. Каждый играющий в команде по очереди участвует в преобразовании геометрической фигуры, добавляя свой элемент, составляя отдельный элемент предмета из нескольких фигур. В заключении дети анализируют свои фигуры, находят сходства и различия в решении конструктивного замысла.

К каждому занятию стараюсь изготовить новую интересную таблицу. А некоторые таблицы использовала несколько раз, но давала уже более сложные задания, различные по цвету, форме и величине. Задание такого характера:

Назовите самый большой треугольник.

Какого цвета самая маленькая фигура?

Назовите все квадраты, начиная с самого маленького и т.п.

Такие же задания дети выполняют в свободное от занятий время, только геометрические фигуры были разложены на столе или на полу. Использование дидактических игр на занятиях и в свободное время способствует закреплению у детей памяти, внимания, мышления. Поэтому в дальнейшем буду продолжать использовать в своей работе различные дидактические игры и упражнения.

В дошкольном возрасте у детей начинают формироваться элементы логического мышления, т.е. формируется умение рассуждать, делать свои умозаключения. Существует множество дидактических игр и упражнений , которые влияют на развитие творческих способностей у детей, так как они оказывают действие на воображение и способствуют развитию нестандартного мышления у детей. Такие игры как найди нестандартную фигуру, чем отличаются, мельница. Они направлены на тренировку мышления при выполнении действий.

С целью развития у детей мышления, я использую различные игры и упражнения.

Это задания на нахождение пропущенной фигуры, продолжения ряды фигур, знаков, на поиск чисел. Знакомство с таким заданиями начала с элементарных заданий на логическое мышление – цепочки закономерностей. В таких упражнениях идет чередование предметов или геометрических фигур. Детям предлагала продолжить ряд или найти пропущенный элемент.

Кроме того давала задания такого характера: продолжить цепочку, чередуя в определенной последовательности квадраты, большие и маленькие круги желтого и красного цвета. После того, как дети научились выполнять такие упражнения, задания для них усложняю. Предлагаю выполнить задания, в котором необходимо чередовать предметы, учитывать одновременно цвет и величину.

В дальнейшем перешла на отвлеченные предметы. Детей очень увлекают игры типа: кого не хватает? Предлагаю детям представить, какой формы могут быть космические существа. Затем показываю плакат, на котором изображены космические “человечки”. Дети находят, какого “человечка” не хватает, анализируют и доказывают. Такие игры помогают развивать у детей умение мыслить логически, сравнивать сопоставлять и высказывать свои умозаключения.

Особое место среди математических игр занимают игры на составление плоскостных изображений предметов, животных, птиц из фигур. Детям нравится составлять изображение по образцу, они радуются свои результатам и стремятся выполнять задания еще лучше.

Для закрепления знаний, полученных на занятиях я даю детям домашние задания в виде дидактических игр и упражнений. Например: собери бусы, найди ошибку, какие цифры потерялись? и т.п.

Дети стараются выполнить свое задание правильно, не допуская ошибок, чтобы получить за это веселое солнышко, а не хмурую тучку с дождиком. Родители тоже очень серьезно относятся к выполнению домашнего задания с детьми. В уголке для родителей выставляю папку с дидактическими играми, объясняя цель и ход игры.

Используя различные дидактические игры в работе с детьми, я убедилась в том, что играя, дети лучше усваивают программный материал, правильно выполняют сложные задания.

Применение дидактических игр повышает эффективность педагогического процесса, кроме того, они способствуют развитию памяти, мышления у детей, оказывая огромное влияние на умственное развитие ребенка. Обучая маленьких детей в процессе игры, стремлюсь к тому, чтобы радость от игр перешла в радость учения.

Учение должно быть радостным!

Поэтому я рекомендую воспитателям старших групп использовать дидактические игры в процессе обучения детей.

Литература

1.Дидактические игры в детском саду А.И.Сорокина

2.Чего на свете не бывает. О.М.Дьяченко, Е.А.Агаева

3.Ступени творчества или развивающие игры Б.П.Никитин

4.Игровые занимательные задачи для дошкольников. З.А.Михайлова

5.Давайте поиграем. А.А.Столяр

6.Математика для дошкольников. Т.И.Еофеев

7.Развитие логического мышления детей. Л.Ф.Тихоморова, А.В.Басов

8.Математика от трех до семи. (Учебно-методическое пособие для воспитателей детских садов).

infourok.ru

классификация дидактических игр по математике. - «Дошколенок.ру»

Дидактические игры по формированию математических представлений условно делятся на следующие группы:

1. Игры с цифрами и числами

2. Игры путешествие во времени

3. Игры на ориентирование в пространстве

4. Игры с геометрическими фигурами

5. Игры на логическое мышление

К первой группе игр относится обучение детей счету в прямом и обратном порядке. Используя сказочный сюжет детей, знакомят с образованием всех чисел в пределах 10, путем сравнивания равных и неравных групп предметов. Сравниваются две группы предметов, расположенные то на нижней, то на верхней полоске счетной линейки. Это делается для того, чтобы у детей не возникало ошибочное представление о том, что большее число всегда находится на верхней полосе, а меньшее на - нижней.

Играя в такие дидактические игры как "Какой цифры не стало?", "Сколько?", "Путаница?", "Исправь ошибку", "Убираем цифры", "Назови соседей", дети учатся свободно оперировать числами в пределах 10 и сопровождать словами свои действия.

Дидактические игры, такие как "Задумай число", "Число как тебя зовут?", "Составь табличку", "Составь цифру", "Кто первый назовет, которой игрушки не стало?" и многие другие используются на занятиях в свободное время, с целью развития у детей внимания, памяти, мышления.

Игра "Считай не ошибись!", помогает усвоению порядка следования чисел натурального ряда, упражнения в прямом и обратном счете. В игре используется мяч. Дети встают полукругом. Перед началом игры воспитателем задается вопрос, в каком порядке (прямом или обратном) считать. Затем бросается мяч и называется число. Тот, кто поймал мяч, продолжает считать дальше, Игра проходит в быстром темпе, задания повторяются многократно, чтобы дать возможность как можно большему количеству детей принять в ней участие. Такое разнообразие дидактических игр, упражнений, используемых на занятиях и в свободное время, помогает детям усвоить программный материал. Для подкрепления порядкового счета помогают таблицы, со сказочными героями, направляющимися к Вини - Пуху в гости. Кто будет первый? Кто идет второй и т.д.

Вторая группа математических игр (игры - путешествие во времени) служит для знакомства детей с днями недели. Объясняется, что каждый день недели имеет свое название. Для того, чтобы дети лучше запоминали название дней недели, они обозначаются кружочками разного цвета. Наблюдение проводится несколько недель, обозначая кружочками каждый день. Это делается специально для того, чтобы дети смогли самостоятельно сделать вывод, что последовательность дней недели неизменна. Детям рассказывается о том, что в названии дней недели угадывается, какой день недели по счету: понедельник - первый день после окончания недели, вторник- второй день, среда - середина недели, четверг - четвертый день, пятница - пятый. После такой беседы предлагаются игры с целью закрепления названий дней недели и их последовательности. Дети с удовольствием играют в игру "Живая неделя." Для игры вызываются к доске 7 детей, пересчитываются по порядку и получают кружочки разного цвета, обозначающие дни недели. Дети выстраиваются в такой последовательности, как по порядку идут дни недели. Например, первый ребенок с желтым кружочком в руках, обозначающий первый день недели - понедельник и т.д.

Затем игра усложняется. Дети строятся с любого другого дня недели. В дальнейшем, можно использовать следующие игры "Назови скорее", "Дни недели", "Назови пропущенное слово", "Круглый год", "Двенадцать месяцев", которые помогают детям быстро запомнить название дней недели и название месяцев, их последовательность.

В третью группу входят игры на ориентирование в пространстве. Пространственные представления детей постоянно расширяются и закрепляются в процессе всех видов деятельности. Задачей педагога является научить детей ориентироваться в специально созданных пространственных ситуациях и определять свое место по заданному условию. При помощи дидактических игр и упражнений дети овладевают умением определять словом положение того или иного предмета по отношению к другому. Например, справа от куклы стоит заяц, слева от куклы - пирамида и т.д. Выбирается ребенок и игрушка прячется по отношению к нему (за спину, справа, слева и т.д.). Это вызывает интерес у детей и организовывает их на занятие. Для того, чтобы заинтересовать детей, чтобы результат был лучше, используются предметные игры с появлением какого-либо сказочного героя. Например, игра "Найди игрушку", - "Ночью, когда в группе никого не было" - говорится детям, - "к нам прилетал Карлсон и принес в подарок игрушки. Карлсон любит шутить, поэтому он спрятал игрушки, а в письме написал, как их можно найти." Затем распечатывается письмо, в котором написано: "Надо встать перед столом воспитателя, пройти 3 шага вправо и т.д. ". Дети выполняют задание, находят игрушку. Затем, задание усложняется - т.е. в письме дается не описание местонахождения игрушки, а только схема. По схеме дети должны определить, где находится спрятанный предмет. Существует множество игр, упражнений, способствующих развитию пространственного ориентирования у детей: "Найди похожую", "Расскажи про свой узор", "Мастерская ковров", "Художник", "Путешествие по комнате" и многие другие игры. Играя в рассмотренные игры дети учатся употреблять слова для обозначения положения предметов.

Для закрепления знаний о форме геометрических фигур детям предлагается узнать в окружающих предметах форму круга, треугольника, квадрата. Например, спрашивается: "Какую геометрическую фигуру напоминает дно тарелки?" ( поверхность крышки стола, лист бумаги т.д.). Проводится игра типа "Лото". Детям предлагаются картинки ( по 3-4 шт. на каждого), на которых они отыскивают фигуру, подобную той, которая демонстрируется. Затем, предлагается детям назвать и рассказать, что они нашли. продолжительность занятие математика дидактическая игра

Дидактическую игру "Геометрическая мозаика" можно использовать на занятиях и в свободное время, с целью закрепления знаний о геометрических фигурах, с целью развития внимания и воображения у детей. Перед началом игры дети делятся на две команды в соответствии с уровнем их умений и навыков. Командам даются задания разной сложности. Например:

- Составление изображения предмета из геометрических фигур (работа по готовому расчлененному образцу)

- Работа по условию (собрать фигуру человека, девочка в платье)

- Работа по собственному замыслу (просто человека)

Рассмотрим дидактические игры для развития логического мышления. В дошкольном возрасте у детей начинают формироваться элементы логического мышления, т.е. формируется умение рассуждать, делать свои умозаключения. Существует множество дидактических игр и упражнений, которые влияют на развитие творческих способностей у детей, так как они оказывают действие на воображение и способствуют развитию нестандартного мышления у детей. Это такие игры как "Найди нестандартную фигуру, чем отличаются?", "Мельница", и другие. Они направлены на тренировку мышления при выполнении действий.

Это задания на нахождение пропущенной фигуры, продолжения ряды фигур, знаков, на поиск чисел. Знакомство с такими играми начинается с элементарных заданий на логическое мышление - цепочки закономерностей. В таких упражнениях идет чередование предметов или геометрических фигур. Детям предлагается продолжить ряд или найти пропущенный элемент. Кроме того даются задания такого характера: продолжить цепочку, чередуя в определенной последовательности квадраты, большие и маленькие круги желтого и красного цвета. После того, как дети научатся выполнять такие упражнения, задания для них усложняются. Предлагается выполнить задание, в котором необходимо чередовать предметы, учитывать одновременно цвет и величину.

blog.dohcolonoc.ru

Дидактические игры по математике - PDF

Транскрипт

1 Дидактические игры по математике Для формирования у дошкольников представлений о геометрических фигурах и форме предмета проводятся следующие дидактические игры: 1. Дидактическая игра "Посмотри вокруг". Детям вначале предлагается назвать геометрические фигуры: прямоугольник, треугольник, круг, квадрат, овал, шар. После закрепления знаний о геометрических фигурах, детям даются следующие задания: 1. Найти предмет прямоугольной формы. 2. Найти предмет треугольной формы. 3. Найти предмет круглой формы. 4. Найти предмет квадратной формы. 6. Найти предмет шарообразной формы. Ребенок ищет эти предметы в аудитории. Выводы: В процессе этой дидактической игры у детей формируются представления о геометрических фигурах и форме предмета. Дети с интересом выполняют данные задания. Благодаря выполнениям этих заданий, дети учатся сопоставлять геометрические фигуры с формой. Так как форма является "эталоном", дети начинают понимать значение слова "эталона". Данная игра позволила закрепить представления о геометрических фигурах, научить детей находить предметы определенной формы в окружении. 2. Дидактическая игра "Почини одеяло". Цель игры знакомство с геометрическими фигурами и составление геометрических фигур из данных. Детям раздаются наборы геометрические фигур и листы цветной бумаги ("одеяло") с обозначенными на нем "дырками". Игра проводится в виде рассказа: "Жил-был Буратино, у которого на кровати лежало красивое одеяло. Однажды Буратино ушел в театр Карабаса-Барабаса, а крыса Шумара в это время прогрызла в одеяле дыры. Детям даются задания: 1. Сосчитать сколько дыр в одеяле. 2. Взять свои фигуры и починить одеяло". Дети раскладывают имеющиеся у них геометрические фигуры куба, квадрата, треугольника и прямоугольника, а также шара и овала на цветные листы бумаги ("одеяла") с обозначенными "дырами". Вывод: Дети активно работали и с интересом участвовали в процессе игры "Почини одеяло". Треугольную форму дети называли самостоятельно, без приведения примера. При этом дети приводили свои примеры а не повторяли примеры своих товарищей. 3. Дидактическая игра "Составные картинки" Цель игры закрепить представления детей о разновидностях геометрических фигур, а также учить детей анализировать изображения предмета сложной формы. Детям раздаются образцы рисунков, составленные из геометрических фигур, а также наборы геометрических фигур. Затем задаются вопросы:

2 1. Что нарисовано на этих картинках? 2. Из каких фигур состоят домик, елочка и т.д.? Затем дети выкладывают из своих геометрических фигур изображения предметов по образцу. 4. Дидактическая игра "Муравьи" Цель: Закрепить представления детей о том, что геометрические фигуры могут быть как большими, так и маленькими. Для игры нужно взять плоскостные изображения черного и красного муравья, а также большие и маленькие плоскостные изображения геометрических фигур. Перед тем как начать игру детям даются следующие пояснения: что большие фигуры это черный муравей, а маленькие красный. Игра начинается с рассказа: "В одном лесу жилибыли красные и черные муравьи. Муравьям нужно было перенести все фигуры в свои домики, но на пути им встречались ворота большие и маленькие. Через какие ворота должны пройти муравьи и почему? В каком домике живет каждый из них?" Выводы: Так при проведении дидактической игры "Муравьи", у детей формируются представления о том, что геометрические фигуры могут быть разными по размеру. Детей в процессе игры привлекала красочность и содержание игры. Благодаря этому дети лучше усвоили и закрепили представления о геометрических фигурах и форме предмета. Составление геометрических фигур Цель: упражнять в составлении геометрических фигур на плоскости стола, анализе и обследовании их зрительно-осязаемым способом. Материал: счётные палочки (15-20 штук), 2 толстые нитки (длина 25-30см) Задания: 1. Составить квадрат и треугольник маленького размера 2. Составить маленький и большой квадраты 3. Составить 2 равных треугольника из 5 палочек 4. Составить 2 равных квадрата из 7 палочек 5. Составить 3 равных треугольника из 7 палочек 6. Составить 4 равных треугольника из 9 палочек 7. Составить 3 равных квадрата из10 палочек 8. Из 5 палочек составить квадрат и 2 равных треугольника 9. Из 9 палочек составить квадрат и 4 треугольника 10. Из 9 палочек составить 2 квадрата и 4 равных треугольника (из 7 палочек составляют 2 квадрата и делят на треугольники 11. Составить прямоугольник, верхняя и нижняя стороны которого будут равны 3 палочкам, а левая и правая Составить из ниток последовательно фигуры: круг и овал, треугольники. Прямоугольники и четырёхугольники. Цепочка примеров Цель: упражнять в умении производить арифметические действия Ход игры: взрослый бросает мяч ребёнку и называет простой арифметический, например 3+2. Ребёнок ловит мяч, даёт ответ и бросает мяч обратно и т.д.

3 Помоги Чебурашке найти и исправить ошибку. Ребёнку предлагается рассмотреть, как расположены геометрические фигуры, в какие группы и по какому признаку объединены, заметить ошибку, исправить и объяснить. Ответ адресуется Чебурашке (или любой другой игрушке). Ошибка может состоять в том, что в группе квадратов может оказаться треугольник, а в группе фигур синего цвета красная. Только одно свойство Цель: закрепить знание свойств геометрических фигур, развивать умение быстро выбрать нужную фигуру, охарактеризовать её. Ход игры: у двоих играющих по полному набору геометрических фигур. Один кладёт на стол любую фигуру. Второй играющий должен положить на стол фигуру, отличающуюся от неё только одним признаком. Так, если 1-й положил жёлтый большой треугольник, то второй кладёт, например, жёлтый большой квадрат или синий большой треугольник. Игра строится по типу домино. Найди и назови Цель: закрепить умение быстро находить геометрическую фигуру определённого размера и цвета. Ход игры: На столе перед ребёнком раскладываются в беспорядке геометрических фигур разного цвета и размера. Ведущий просит показать различные геометрические фигуры, например: большой круг, маленький синий квадрат и т.д. Игры с геометрическими фигурами. Игра «Чудесный мешочек» хорошо знакома дошкольникам. Она позволяет обследовать геометрическую форму предметов, упражняться в различении форм. В мешочке находятся предметы разных геометрических фигур. Ребенок обследует их, ощупывает и называет фигуру которую хочет показать. Усложнить задание можно, если ведущий дает задание найти в мешочке какую-то конкретную фигуру. При этом ребенок последовательно обследует несколько фигур, пока не отыщет нужную. Этот вариант задания выполняется медленнее. Поэтому целесообразно, чтобы чудесный мешочек был у каждого ребенка. Игра «Найди такой же» перед детьми лежат карточки, на которых изображены три- четыре различные геометрические фигуры. Воспитатель показывает свою карточку (или называет, перечисляет Фигуры на карточке). Дети должны найти такую же карточку и поднять ее. Игра «Кто больше увидит?» На доске в произвольном порядке расположены различные геометрические фигуры. Дошкольники рассматривают и запоминают их. Ведущий считает до трех и закрывает фигуры. Детям предлагают назвать как можно больше фигур, размещенных на фланелеграфе. Что бы дети не повторяли ответы товарищей ведущий может выслушивать каждого ребёнка отдельно. Выигрывает тот кто запомнит и назовет больше фигур он становится ведущим. Продолжая игру ведущий меняет количество фигур Игра «Посмотри вокруг» помогает закрепить представления о геометрических фигурах, учит находить предметы определенной формы. Игра проводится в виде соревнования на личное или командное первенство. В этом случае группа делится на команды. Ведущий ( им может быть воспитатель или ребенок) предлагает назвать предметы

4 круглой, прямоугольной, квадратной, четырехугольной формы, форму предметов, не имеющих углов, и т.д. За каждый правильный ответ играющий или команда получает фишку, кружок. Правилами предусматривается, что нельзя называть два раза один и тот же предмет. Игра проводится в быстром темпе. В конце игры подводятся итоги, называется победитель, набравший наибольшее количество очков. Игра «Геометрическая мозаика» предназначена для закрепления у детей знания о геометрических фигурах, формирует умение преобразовывать их, развивает воображение и творческое мышление,, учит анализировать способ расположения частей, составлять фигуру, ориентироваться на образец. Организуя игру, воспитатель заботится об объединении детей в одну команду в соответствии с уровнем их умений и навыков. Команды получают задания разной трудности. На составление изображения предмета из геометрических фигур: работа по готовому расчлененному образцу, работа по нерасчлененному образцу, работа по условиям (собрать фигуру человека девочка в платье), работа по собственному замыслу (просто человека). Каждая команда получает одинаковые наборы геометрических фигур. Дети должны самостоятельно договориться о способах выполнения задания, о порядке работы, выбрать исходный материал. Каждый играющий в команде по очереди участвует в преобразовании геометрической фигуры, добавляя свой элемент, составляя отдельные элементы предмета из нескольких фигур. В заключении игры дети анализируют свои фигуры, находят сходства и различия в решении конструктивного замысла. Игра «Найди свой домик». Дети получают по одной модели геометрической фигуры и разбегаются по комнате. По сигналу ведущего все собираются у своего домика с изображением фигуры. Усложнить игру можно переместив домик. Детей учат видеть геометрическую форму в окружающих предметах: мяч, арбуз-шар, тарелка, блюдце- обруч- круг, крышка стола, стена, пол, потолок, окно-прямоугольник, платок квадрат; косынка-треугольник; стакан- цилиндр; яйцо, кабачок- овал. Игра «Величина». Что бывает широкое (длинное, высокое, низкое, узкое) Цель. Уточнить представление детей о величине предметов, учит находить сходство предметов по признаку величины. Ход игры. Взрослый говорит: «Предметы, которые нас окружают, бывают разной величины: большие, маленькие, длинные, короткие, низкие, высокие, узкие, широкие. Мы видели много разных по величине предметов. А сейчас мы поиграем так: я буду называть одно слово, а ты будешь перечислять, какие предметы можно назвать этим одним словом». В руках у взрослого мяч. Он бросает его ребёнку и говорит слово. Например: Взрослый: Длинный Ребёнок: Дорога, лента, верёвка и т.д. Игра с двумя наборами. Цель. Учить детей сравнивать предметы по величине путём накладывания одного на другой, находить два предмета одинаковой величины. Материал: две одинаковые пирамидки. Ход игры. «Давай вместе поиграем», - обращается взрослый к ребёнку и начинает снимать кольца с пирамидки, предлагая ребёнку сделать то же. «А теперь найди такое же кольцо», - говорит взрослый и показывает одно из колец. Когда ребёнок выполнит это задание, взрослый предлагает сравнить кольца путём накладывания. а затем продолжить игру кем либо из детей.

5 Игра «Кто работает рано утром?» Это игра- путешествие. Она начинается чтением стихотворения Б.Яковлева из книги «Утро, вечер, день, ночь» Если звонко за окном Защебечут птицы, Если так светло кругом, Что тебе не спится, Если радио у вас Вдруг заговорило, Это значит, что сейчас Утро наступило. Взрослый: «Теперь мы с тобой будем вместе путешествовать и смотреть, кто и как работает утром». Взрослый помогает ребёнку вспомнить, кто раньше всех начинает работать (дворник, водители общественного транспорта и т.д.) Вспомните вместе с ребёнком, а что делают утром дети и взрослые. Закончит путешествие можно чтением стихотворения Б. Яковлева или обобщением того, что происходит рано утром. «Вчера, сегодня, завтра» Взрослый и ребёнок встают напротив друг друга. Взрослый бросает мяч ребёнку и говорит короткую фразу. Ребёнок должен назвать соответствующее время и бросить мяч взрослому. Например: Мы лепили (вчера). На прогулку идём (сегодня) и т.д. Дидактические игры «Геометрические фигуры» Игра «Назови геометрическую фигуру» Цель. Учить зрительно обследовать, узнавать и правильно называть плоскостные геометрические фигуры (круг, квадрат, треугольник, прямоугольник, овал) Материал. Таблицы с геометрическими фигурами. На каждой таблице контурные изображения двух-трёх фигур в разных положениях и сочетаниях. Ход игры. Игра проводится с одной таблицей. Остальные можно закрыть чистым листом бумаги. Взрослый предлагает внимательно рассмотреть геометрические фигуры, движением руки обвести контуры фигур, назвать их. На одном занятии можно показать ребёнку 2-3 таблицы. Игра «Найди предмет такой же формы» У взрослого имеются нарисованные на бумаге геометрические фигуры: круг, квадрат, треугольник, овал, прямоугольник и т.д. Он показывает ребёнку одну из фигур, например, круг. Ребёнок должен назвать предмет такой же формы. Игра «Угадай, что спрятали» На столе перед ребёнком карточки с изображением геометрических фигур. Ребёнок внимательно их рассматривает. Затем ребёнку предлагают закрыть глаза, взрослый прячет одну карточку. После условного знака ребёнок открывает глаза и говорит, что спрятано.

6 Цепочка примеров Цель: упражнять детей в умении производить арифметические действия. Ход игры: две группы участников садятся на стулья одна против другой. Один ребенок берет мяч, называет простой арифметический пример: и бросает мяч кому-нибудь из другой группы. Тот, кому брошен мяч, дает ответ и бросает мяч игроку из первой группы. Поймавший мяч продолжает пример, в котором надо произвести действие с числом, являющимся ответом в первом примере. Участник игры, давший неверный ответ или пример, выбывает из игры. Выигрывает группа детей, у которой осталось больше игроков (предлагается для детей 6 7 лет, успешно усвоившими арифметические действия). Отгадай число Цель: закрепить умение детей сравнивать числа. Ход игры: по заданию ведущего ребенок должен быстро назвать число (числа) меньше 8, но больше 6; больше 5, но меньше 9 и т.д. Ребенок, выполнивший условия игры, получает флажок. При делении детей на 2 группы ответивший неправильно выбывает из игры. Только одно свойство Для игры необходимо изготовить специальный набор геометрических фигур. В него входят 4 фигуры (круг, квадрат, треугольник и прямоугольник) четырех цветов (красного, синего, желтого и белого), маленького размера. В этот же набор включается такое же количество перечисленных фигур указанных цветов, но больших по размеру. Таким образом, для игры (на одного участника) необходимо 16 маленьких геометрических фигур четырех видов и четырех цветов и столько же больших. Цель: закрепить знание свойств геометрических фигур, развивать умение быстро выбирать нужную фигуру, описывая ее. Ход игры: у двоих играющих детей по полному набору фигур. Один (тот, кто начинает игру) кладет на стол любую фигуру. Второй играющий должен положить рядом фигуру, отличающуюся от нее только по одному признаку. Так, если первый положил желтый большой треугольник, то второй кладет желтый большой квадрат или синий большой треугольник и т.д. Неправильным считается ход, если второй играющий положит фигуру, не отличающуюся от нее более чем на один признак. В этом случае фигуру у игрока забирают. Проигрывает тот, кто первый останется без фигур. (Возможны варианты.) Игра строится по типу домино. По ходу игры требуется быстрая ориентировка играющих в цвете, форме, размере фигур, отсюда и воздействие на развитие логики, обоснованности мышления и действий. Числовой ряд (для детей старшего дошкольного возраста) Цель: закрепить знание последовательности чисел в натуральном ряду. Ход игры: двое детей раскладывают перед собой лицевой стороной вниз карточки с цифрами то 1 до 10. При этом каждому из детей дается определенное количество карточек с цифрами (например, до 13). Некоторые из цифр встречаются в наборе дважды. Каждый играющий в порядке очередности берет карточку с цифрой, открывает ее и кладет перед собой.

7 Затем первый играющий открывает еще одну карточку. Если обозначенное на ней число меньше числа открытой им ранее карты, ребенок кладет карточку левее первой, если больше правее. Если же возьмет карту с числом уже открытым, то возвращает ее на место, а право ходе переходит соседу. Выигрывает тот, кто первый выложит свой ряд. Назови число Цель: упражнять детей в умении производить устные вычисления. Ход игры: взрослый или старший ребенок говорит: «я могу отгадать число, которое ты задумал. Задумай число, прибавь к нему 6, от суммы отними 2, затем еще отними задуманное число, к результату прибавь 1, у тебя получилось число 5». В этой несложной задаче на смекалку задуманное число может быть любым, но для решения ее нужно уметь устно вычислять. Сколько взять конфет? Цель: упражнять детей в соотнесении условия задачи с результатом. Ход игры: предлагается условие задачи: «в вазе лежало 3 яблоко. Мама угостила ими трех девочек. Каждая из девочек получила по одному яблоку, и одно осталось в вазе. Как это получилось?» к ответу решающей задачу приходит вследствие размышления, соотнесения условий с результатом. (одна девочка взяла яблоко вместе с вазой).

docplayer.ru

90	75	71	63	66
67	82	86	68	76
87	61	73	89	81
74	88	65	77	84
80	69	78	62	70
64	83	72	79	85

90	75	71	63	66
67	82	86	68	76
87	61	73	89	81
74	88	65	77	84
80	69	78	62	70
64	83	72	79	85

90	75	71	63	66
67	82	86	68	76
87	61	73	89	81
74	88	65	77	84
80	69	78	62	70
64	83	72	79	85

90	75	71	63	66
67	82	86	68	76
87	61	73	89	81
74	88	65	77	84
80	69	78	62	70
64	83	72	79	85

90	75	71	63	66
67	82	86	68	76
87	61	73	89	81
74	88	65	77	84
80	69	78	62	70
64	83	72	79	85

90	75	71	63	66
67	82	86	68	76
87	61	73	89	81
74	88	65	77	84
80	69	78	62	70
64	83	72	79	85