Внеурочное занятие "Симметрия в живой и неживой природе". Красота и симметрия бабочек
Проект «Бабочки – это красиво и интересно!»
Конференция «Проектная деятельность в образовательном учреждении - 2014»
Номинация «Детский проект в начальной школе»
Однажды летом я приехала в гости к бабушке. У неё было посажено очень, много цветов, а над ними порхали бабочки. Это было так красиво! Я и раньше видела этих прекрасных насекомых, но не в таком большом количестве. Поэтому, наверное, и не обращала на них внимания. Ну, летают себе и летают. Я стала их рассматривать и мне захотелось узнать больше о бабочках. Изучению этих красивейших насекомых посвящен мой проект.
Цель проекта: Изучение основных особенностей строения, жизнедеятельности и развития бабочек.
Задачи:
1. Узнать из различных источников о видах, развитии бабочек и жизнедеятельности.
2. Понаблюдать за жизнью бабочек, узнать в чем их польза и вред.
3. Провести опрос моих одноклассников и сделать выводы.
Актуальность: бабочки очень красивые насекомые и часто привлекают наше внимание.
Гипотеза 1: Бабочка в своем развитии проходит несколько стадий превращений.
Гипотеза 2: Бабочки очень красивые и разнообразные, встречаются очень часто, радуют нас и приносят пользу.
Объект исследований: бабочка.
Предмет исследования: процесс развития бабочки.
Приложение: буклет «Прекрасное рядом. Бабочки».
В ходе исследования мои гипотезы подтвердились.
- Бабочка в своем развитии проходит 4 стадии превращений. Яйцо – личинка или гусеница – куколка – бабочка.
- Бабочка очень красивая, поэтому радует нас и приносит пользу, а гусеницы еще приносят и вред.
Надо беречь это хрупкое и прекрасное создание!
Мне было интересно проводить исследование. Я подробно узнала о строении и жизнедеятельности бабочки, их видах. Бабочек так много! Научилась замечать бабочек в повседневной жизни.
- Новогодний костюм у меня был «бабочка».
- Много бабочек я сделала из бумаги.
- На одежде тоже встречается очень много бабочек в виде рисунков.
- Заколки, бантики в виде бабочек.
- Я сама украсила футболку бабочками.
- Моя сестра занимается плаванием. Она тоже встречалась с бабочками. Один из стилей плавания «баттерфляй» переводится как «бабочка».
Можно собрать огромную коллекцию бабочек и посвятить их изучению целую жизнь. А я постараюсь летом самостоятельно вывести бабочку в домашних условиях.
Мою работу можно использовать на уроках окружающего мира, изобразительного искусства, литературного чтения. Мне встретилось множество стихотворений, рассказов про бабочек.
Помогали мне проводить исследования и оформлять работу моя мама и учитель. Большое им спасибо!
Приложение 1. Проект «Бабочки – это красиво и интересно!»
Приложение 2. Презентация проекта.
Авторизуйтесь на сайте, чтобы скачать файл
Авторизуйтесь на сайте, чтобы скачать файл
Автор: Индюкова Анна, обучающаяся 1 класса МБОУ Гимназия №9, город Химки Московской области. Руководитель: Гущенская Ирина Петровна, учитель начальных классов высшей квалификационной категории МБОУ Гимназия № 9, город Химки Московской области.
Авторизуйтесь на сайте, чтобы вы могли оставить свой комментарий.
Симметрия Проектно-исследовательская работа
Симметрия.
Проектно–исследовательская работа.
Авторы: Сухова Анастасия, Краснова Анна, ученицы 8 класса МОУ СОШ №4.
Руководитель: учитель математики О. А. Куликова.
Выдвижение Формулировка проблемы. В чём заключается проблема? На какой вопрос предстоит ответить?
Цель исследования.
Целью нашей работы является изучение многообразия симметрии и ее использование. Выяснить: «Симметрия это –
гармония и красота?
равновесие?
устойчивость?»
Задачи исследования:
Найти симметричные фигуры и предметы в окружающем мире.
Доказать, что действительно нас окружают симметричные предметы.
Определить значение использования симметрии.
Для решения поставленных задач я должен провести собственное исследование:
Изучить внешний вид насекомых, растений, птиц, животных, зданий, предметов быта.
Показать пути использования симметрии в жизни человека.
гипотезы. Каким может быть предположительный ответ?
Симметрия является той идеей,
посредством которой человек на протяжении веков пытался
постичь и создать порядок,
красоту и совершенство.
Г. Вейль.
Актуальность исследования.
В наше время, наверное, трудно найти человека, который не имел бы какого-либо представления о симметрии. Мир, в котором мы живем, наполнен симметрией домов и улиц, гор и полей, творениями природы и человека. С симметрией мы встречаемся буквально на каждом шагу: в природе, технике, искусстве, науке. Понятие симметрии проходит через всю многовековую историю человеческого творчества. Оно встречается уже у истоков человеческого развития. Издавна человек использовал симметрию в архитектуре. Древним храмам, башням средневековых замков, современным зданиям она придает гармоничность, законченность.
В настоящее время ученые расширяют свои учения о симметрии. Добавляются новые обширные разделы, такие как цветная симметрия, симметрия многомерных пространств и другие. Свои новые результаты они излагают в монографиях. Значит, выбранная нами тема актуальна.
Определение предмета исследования.
Понятие симметрия проходит через многовековую историю человеческого творчества.
Симметрию можно обнаружить почти везде, если знать, как ее искать. Если посмотреть на листья, бабочку, снежинку, то можно увидеть, что их объединяет то, что они симметричны. Также симметрию можно увидеть в природе, в предметах домашнего обихода, в предметах, которых создал человек. Творчество людей во всех своих проявлениях тяготеет к симметрии. Действительно, симметричные объекты окружают нас со всех сторон, мы имеем дело с симметрией везде. Посредством симметрии человек пытался, по словам немецкого математика Германа Вейля, «постичь и создать порядок, красоту и совершенство». Это же имел в виду и французский архитектор Ле Карбюзье, когда писал, что «человеку необходим порядок; без него все действия теряют согласованность, логическую взаимосвязь…». Получается, что симметрия – это уравновешенность, упорядоченность, красота, совершенство.
Осевая симметрия — тип симметрии, имеющий два несколько отличающихся определения:
Отражательная симметрия. В математике осевая симметрия — вид движения, при котором множеством неподвижных точек является прямая, называемая осью симметрии. Например, плоская фигура прямоугольник в пространстве осе симметрична и имеет 3 оси симметрии (две — в плоскости фигуры), если это не квадрат.
Вращательная симметрия. В естественных науках под осевой симметрией понимают вращательную симметрию(другие относительно поворотов вокруг прямой. При этом тело (фигуру, задачу, организм) называют осе симметричными, если они переходят в себя при любом(например, малом) повороте вокруг этой прямой. В этом случае, прямоугольник не будет осе симметричным телом, но конус будет.
Центральной симме́три́ей относительно точки A называют преобразование пространства, переводящее точку X в такую точку X1, что A — середина отрезка XX1. Центральная симметрия с центром в точке A обычно обозначается через ZA, в то время как обозначение SA можно перепутать с осевой симметрией. Фигура называется симметричной относительно точки A, если для каждой точки фигуры симметричная ей точка относительно точки A также принадлежит этой фигуре. Точка A называется центром симметрии фигуры. Говорят также, что фигура обладает центральной симметрией.
Фигуры обладающие осевой симметрией. У неразвёрнутого угла одна ось симметрии — прямая, на которой расположена биссектриса угла.
Равнобедренный (но не равносторонний) треугольник имеет также одну ось симметрии. А равносторонний треугольник — три основные симметрии.
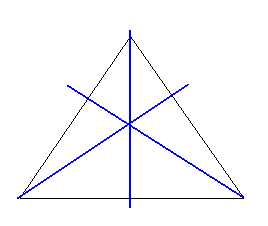
Прямоугольник и ромб, не являющиеся квадратами имеют по две оси симметрии, а квадрат — четыре оси симметрии.
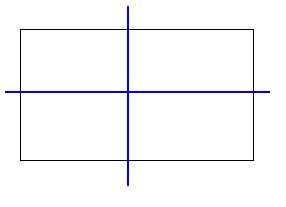
У окружности их бесконечно много — любая прямая, проходящая через её центр, является осью симметрии.
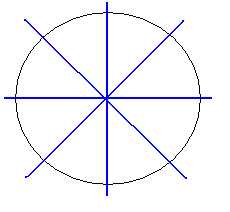
Имеются фигуры, у которых нет ни одной оси симметрии, например, разносторонний треугольник. Центральная симметрия. 1. Отрезок имеет две оси симметрии (серединный перпендикуляр и прямая, содержащая этот отрезок) и центр симметрии (середина).
2. Треугольник общего вида не имеет осей или центров симметрии, он несимметричен. Равнобедренный (но не равносторонний) треугольник имеет одну ось симметрии: серединный перпендикуляр к основанию.
3. Равносторонний треугольник имеет три оси симметрии (серединные перпендикуляры к сторонам) и поворотную симметрию относительно центра с углом поворота 120.
4. У любого правильного n-угольника есть n осей симметрии, все они проходят через его центр. Он также имеет поворотную симметрию относительно центра с углом поворота.
Математики о симметрии
Математик любит прежде всего симметрию
Максвелл Д.
Красота тесно связана с симметрией
Вейль Г.
Симметрия … является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство
Вейль Г.
Для человеческого разума симметрия обладает, по — видимому, совершенно особой притягательной силой
Фейнман Р.
Симметрия в исскустве
Художники разных эпох использовали симметричное построение картины. Такое построение позволяет достигнуть впечатление покоя, величественности, особой торжественности и значимости событий. В симметричной коипозиции люди или предметы расположены почти зеркально по отношению к центральной оси картины. Симметрия в искусстве основана на реальной действительности, изобилующей симметрично устроенными формами. Например, симметрична устроена фигура человека, бабочка, снежинка и многое другое. Симметричные картины - статичные (устойчивые), левая и правая половины уравновешены. В асимметричной композиции расположение объектов может быть самым разнообразным в зависимости от сюжета и замысла произведения, левая и правая половины не уравновешены. Композицию натюрморта или пейзажа легко представить в виде схемы, на которой ясно видно, симметрична или асимметрична построена композиция.
Симметрия в искусстве вообще и в изобразительном в частности берет свое начало в реальной действительности, изобилующей симметрично устроенными формами.
Для симметричной организации композиции характерна уравновешенность ее частей по массам, по тону, цвету и даже по форме. В таких случаях одна часть почти зеркально похожа на вторую. В симметричных композициях чаще всего имеется ярко выраженный центр. Как правило, он совпадает с геометрическим центром картинной плоскости. Если точка схода смещена от центра, одна из частей более загружена по массам или изображение строится по диагонали, все это сообщает динамичность композиции и в какой-то мере нарушает идеальное равновесие.
Правилом симметрии пользовались еще скульпторы Древней Греции. Примером может служить композиция западного фронтона храма Зевса и Олимпии. В основу ее положена борьба лапифов (греков) с кентаврами в присутствии бога Аполлона. Движение постепенно усиливается от краев к центру. Оно достигает предельной выразительности в изображении двух юношей, которые замахнулись на кентавров. Нарастающее движение как бы сразу обрывается на подступах к фигуре Аполлона, спокойно и величественно стоящего в центре фронтона.
Представление об утраченных произведениях знаменитых живописцев V века до н. э. можно составить по античной вазописи и помпейским фрескам, навеянным, как полагают исследователи, произведениями греческих мастеров эпохи классики…
Симметричные композиции наблюдались и у греческих мастеров IV-III веков до н. э. Об этом можно судить по копиям фресок. В помпейских фресках главные фигуры находятся в центре пирамидальной композиции, отличающейся симметрией.
К правилам симметрии нередко прибегали художники при изображении торжественных многолюдных собраний, парадов, заседаний в больших залах и т. д.
Большое внимание правилу симметрии уделяли художники раннего Возрождения, о чем свидетельствует монументальная живопись (например, фрески Джотто). В эпоху Высокого Возрождения итальянская композиция достигла зрелости. Например, в картине «Святая Анна с Марией и младенцем Христом» Леонардо да Винчи компонует три фигуры в заостренный кверху треугольник. В правом нижнем углу он дает фигурку агнца, которого держит маленький Христос. Все скомпоновано таким образом, что этот треугольник только угадывается под объемно-пространственной группой фигур.
Симметричной композицией можно назвать и «Тайную вечерю» Леонардо да Винчи. В этой фреске показан драматический момент, когда Христос сообщил своим ученикам: «Один из вас предаст меня». Психологическая реакция апостолов на эти вещие слова связывает персонажей с композиционным центром, в котором находится фигура Христа. Впечатление целостности от этой центростремительной композиции усиливается еще и тем, что художник показал помещение трапезной в перспективе с точкой схода параллельных линий в середине окна, на фоне которого четко рисуется голова Христа. Таким образом, взор зрителя невольно направляется к центральной фигуре картины.
Среди произведений, демонстрирующих возможности симметрии, можно также назвать «Обручение Марии» Рафаэля, где нашли наиболее полное выражение приемы композиции, характерные для эпохи Возрождения.
Картина В. М. Васнецова «Богатыри» также построена на основе правила симметрии. Центром композиции является фигура Ильи Муромца. Слева и справа, как бы в зеркальном отражении, размещены Алеша Попович и Добрыня Никитич. Фигуры расположены вдоль картинной плоскости спокойно сидящими на конях. Симметричное построение композиции передает состояние относительного покоя. Левая и правая фигуры по массам неодинаковы, что обусловлено идейным замыслом автора. Но обе они менее мощные по сравнению с фигурой Муромца и в целом придают полное равновесие композиции.
Устойчивость композиции вызывает у зрителя чувство уверенности в непобедимости богатырей, защитников земли русской. Мало того, в «Богатырях» передано состояние напряженного покоя на грани перехода в действие. А это значит, что и симметрия несет в себе зародыш динамического движения во времени и пространстве.
Симметрия в химии
Симметрия в химии проявляется в геометрической конфигурации молекул, что сказывается на специфике физических и химических свойств молекул в изолированном состоянии, во внешнем поле и при взаимодействии с другими атомами и молекулами.
Большинство простых молекул обладает элементами пространственной симметрии равновесной конфигурации: осями симметрии, плоскостями симметрии и т. д. (см. Симметрия в математике). Так, молекула аммиака Nh4 обладает симметрией правильной треугольной пирамиды, молекула метана Ch5 - симметрией тетраэдра. У сложных молекул симметрия равновесной конфигурации в целом, как правило, отсутствует, однако приближённо сохраняется симметрия отдельных её фрагментов (локальная симметрия). Наиболее полное описание симметрии как равновесных, так и неравновесных конфигураций молекул достигается на основе представлений о т. н. динамических группах симметрии — группах, включающих не только операции пространственной симметрии ядерной конфигурации, но и операции перестановки тождественных ядер в различных конфигурациях. Например, динамическая группа симметрии для молекулы Nh4 включает также и операцию инверсии этой молекулы: переход атома N с одной стороны плоскости, образованной атомами Н, на другую её сторону.
Симметрия равновесной конфигурации ядер в молекуле влечёт за собой определённую симметрию волновых функций различных состояний этой молекулы, что позволяет проводить классификацию состояний по типам симметрии. Переход между двумя состояниями, связанный с поглощением или испусканием света, в зависимости от типов симметрии состояний может либо проявляться в молекулярном спектре, либо быть запрещенным, так что соответствующая этому переходу линия или полоса будет отсутствовать в спектре. Типы симметрии состояний, между которыми возможны переходы, влияют на интенсивность линий и полос, а также и на их поляризацию. Например, у гомоядерных двухатомных молекул запрещены и не проявляются в спектрах переходы между электронными состояниями одинаковой чётности, электронные волновые функции которых ведут себя одинаковым образом при операции инверсии; у молекул бензола и аналогичных соединений запрещены переходы между невырожденными электронными состояниями одного и того же типа симметрии и т. п. Правила отбора по симметрии дополняются для переходов между различными состояниями правилами отбора, связанными со спином этих состояний.
У молекул с парамагнитными центрами симметрия окружения этих центров приводит к определённому типу анизотропии g-фактора (Ланде множитель), что сказывается на структуре спектров электронного парамагнитного резонанса, тогда как у молекул, ядра атомов которых обладают ненулевым спином, симметрия отдельных локальных фрагментов ведёт к определённому типу расщепления по энергии состояний с различными проекциями ядерного спина, что сказывается на структуре спектров ядерного магнитного резонанса.
В приближённых подходах квантовой химии, использующих представление о молекулярных орбиталях, классификация по симметрии возможна не только для волновой функции молекулы в целом, но и для отдельных орбиталей. Если у равновесной конфигурации молекулы имеется плоскость симметрии, в которой лежат ядра, то все орбитали этой молекулы разбиваются на два класса: симметричные (s) и антисимметричные (p) относительно операции отражения в этой плоскости. Молекулы, у которых верхними (по энергии) занятыми орбиталями являются p-орбитали, образуют специфические классы ненасыщенных и сопряжённых соединений с характерными для них свойствами. Знание локальной симметрии отдельных фрагментов молекул и локализованных на этих фрагментах молекулярных орбиталей позволяет судить о том, какие фрагменты легче подвергаются возбуждению и сильнее меняются в ходе химических превращений, например при фотохимических реакциях.
Представления о симметрии имеют важное значение при теоретическом анализе строения комплексных соединений, их свойств и поведения в различных реакциях. Теория кристаллического поля и теория поля лигандов устанавливают взаимное расположение занятых и вакантных орбиталей комплексного соединения на основе данных о его симметрии, характер и степень расщепления энергетических уровней при изменении симметрии поля лигандов. Знание одной лишь симметрии комплекса очень часто позволяет качественно судить о его свойствах.
В 1965 P. Вудворд и Р. Хоффман выдвинули принцип сохранения орбитальной симметрии при химических реакциях, подтвержденный впоследствии обширным экспериментальным материалом и оказавший большое влияние на развитие препаративной органической химии. Этот принцип (правило Вудворда — Хоффмана) утверждает, что отдельные элементарные акты химических реакций проходят с сохранением симметрии молекулярных орбиталей, или орбитальной симметрии. Чем больше нарушается симметрия орбиталей при элементарном акте, тем труднее проходит реакция.
Симметрия в природеУчёт симметрии молекул важен при поиске и отборе веществ, используемых при создании химических лазеров и молекулярных выпрямителей, при построении моделей органических сверхпроводников, при анализе канцерогенных и фармакологически активных веществ и т. д.
«Симметрия» — такая тема, о которой можно говорить и высоким слогом поэзии, и лаконичным языком математики. Приведём слова поэта Валерия Брюсова из произведения «Сонет к форме», которые как нельзя лучше характеризуют всеобщность симметрии: «Есть тонкие властительные связи…» Можно сказать, что симметрия властвует и в природе, и в искусстве, и в науке, и в других областях человеческой деятельности.
Можно любоваться листьями и цветами, понаблюдать за бабочками на лугу, присмотреться к снежинкам на окнах, узорам на коврах, причудливой резьбе на храмах и соборах; вглядеться в изумительную красоту памятников архитектуры прошедших эпох или просто обратить внимание на современные здания, машины, привычные предметы нашего быта и… увидеть во всём этом проявление законов симметрии.
Когда мы собирали ягоды (смородину, рябину, черемуху), мы обратили внимание на то, что они центрально симметричны (рисунок 4). Действительно, когда мы их разрезали, то увидели, что в разрезе они представляют собой окружность, а окружность, как нам известно, имеет центр симметрии.
Также мы остановились на цветах, которых выращивают наши мамы. Нас привлекло внимание виолы, нарциссы, фиалки. Виолы и фиалки (рисунок №5) обладают осевой симметрией. А цветы нарцисса (рисунок №6) являются центрально симметричными. Из литературы я узнал, что центральной симметрией обладают цветок одуванчика, мать- и — мачехи, цветок кувшинки. Симметричные цветы более привлекательны для пчел, так как у них больше нектара.
Выводы:
В любом растении можно найти какую — то часть, обладающую осевой, центральной симметрией.
Центральная симметрия характерна для плодов растений и некоторых цветов.
Симметрия форм придает им красоту.
II. Симметрия в животном мире.
Теперь мы хотим остановиться на животном мире и выяснить, как связан животный мир и симметрия.
Вот над поляной порхает яркая бабочка. Ее крылышки кажутся совершенно одинаковыми. Как бы для того, чтобы подтвердить это, она садится на цветок, складывает их, и мы видим, что форма одного крыла в точности повторяет форму другого.
Если мы нарисуем бабочку на листе бумаги, то особую роль для этой плоской фигуры будет играть вертикальная прямая, проходящая посередине туловища бабочки. По обе стороны от этой прямой на одинаковом расстоянии от неё находятся одинаковые элементы рисунка. В этом случае говорят, что данная плоская фигура симметрична относительно прямой, а прямую, которая разделяет фигуру на правую и левую половины, называют осью симметрии. В раскраске бабочки можно обнаружить небольшие отклонения. Поэтому говорят, что симметрия бабочки не является математически точной.
Животные симметричны слева направо, а не сверху вниз. Это называют двусторонней симметрией. Животных эволюционировали таким образом из-за необходимости быть устойчивыми и способными к быстрому движению. Если бы животные были не симметричные, т. е., например, имели бы две ноги с одной стороны и одну с другой, им было бы очень сложно балансировать или быстро передвигаться. Неустойчивый и медлительный представитель не может уйти от хищника и с трудом добывает себе пропитание.
Симметрия в архитектуре
Симметрию можно назвать залогом успеха в строительстве. Почти все здания в мире, во избежание разрушения, строятся исключительно симметрично. Вот почему симметрия так важна в строительстве.
Архитектура – удивительная область человеческой деятельности. В ней тесно переплетены и строго уравновешены наука, техника, искусство. Только соразмерное, гармоничное сочетание этих начал делает возводимое человеком сооружение памятником архитектуры. Архитектурный облик здания архитектор создает с помощью строительного материала, образ же его созидается творческим мышлением. Одним из художественных средств, которые он использует, является композиция здания. От неё в первую очередь зависит впечатление, которое оставляет архитектурное сооружение Элементы симметрии можно увидеть в общих планах зданий, архитектуры фасадов, в оформлении внутренних помещений, колоннах, потолках и т.д. В большинстве случаев они обладают осевой симметрией.
Симметрия в нашем городе Шатура
Мы хотим рассказать о нашем наблюдении. Недавно мы гуляли по нашему городу. Прогуливаясь по улицам города, мы сделали несколько снимков. Рассматривая эти фотографии, мы пришли к выводу, что большинство архитектурных сооружений нашего города имеют ось симметрии. Если разбить строение на маленькие пристройки, мы обнаружим, что они обладают осевой симметрией. Сравнивая фасады зданий, имеющие и не имеющие ось симметрии, мы пришли к выводу, что с симметричной композицией здания ясны и уравновешенны. Симметрия придает гармоничность, законченность.
Выводы:
Симметрия широко используется в архитектуре.
Использование симметрии при строении зданий и домов создают красоту и гармонию.
Симметрия в русском языке
Симметрия используется в таких видах искусства, как литература, русский язык, музыка, балет, ювелирное искусство.
Если присмотреться к печатным буквам М, П, Т, Ш, В, Е, З, К, С, Э, Ж, Н, О, Ф, Х, можно увидеть, что они симметричны. Причем у первых четырех ось симметрии проходит вертикально, а у следующих шести – горизонтально, а буквы Ж, Н, О, Ф, Х имеют по две оси симметрии. Симметрию можно увидеть и в целых словах, таких, как «казак», «шалаш» — они читаются одинаково как слева направо, так и справа налево. А вот целые фразы с таким свойством (если не учитывать пробелы между словами): «Искать такси», «Аргентина манит негра», «Ценит негра аргентинец», «Леша на полке клопа нашел». Такие фразы и слова называются палиндромами.
В литературных произведениях существует симметрия образов, положений, мышлений. Вспомним хотя бы закон возмездия в греческой трагедии, где виновный становится жертвой такого же преступления. В «Евгении Онегине» А.С. Пушкина мы наблюдаем симметрию положений: Онегин, отвергнувший когда-то любовь Татьяны, сам через несколько лет был вынужден испытать горечь отвергнутой любви. В трагедии А.С. Пушкина «Борис Годунов» прекрасно выписана симметрия образов. Убийцу царственного наследника сменяет на троне такой же умный, такой же наглый и беспощадный убийца юноши царевича.
В музыке ряд музыкальных форм строятся симметрично. В знаменитых фуэте балерина вращается на одной ножке 6 раз, 12 … 32 раза! Эти движения однотипны, и именно их повторяемость порождает эстетический эффект, служащий достойным завершением танца.
Одно из лучших ранних произведений Рафаэля – «Обручение Марии» — создано в 1504 году (рисунок №2). Симметрия придает картине ясную упорядоченность, движением персонажей завершенность. Под солнечным голубым небом раскинулась долина, увенчанная белокаменным храмом. На первом плане – обряд обручения. Первосвященник сближает руки Марии и Иосифа. За Марией – группа девушек, за Иосифом – юноши. Обе части симметричной композиции скреплены встречным.
Оказывается, симметрия используется не только в математике, но и в русском языке и литературе, в балете.
Выводы
В ходе исследования мы рассмотрели несколько направлений:
Симметрия в архитектуре;
Симметрия в буквах и словах;
Симметрия в природе;
Симметрия в исскустве
Исследования, проведенные мной, показали, что симметрия является одним из принципов гармонического построения мира. «Сфера влияния» симметрии поистине безгранична. Всюду она определяет гармонию природы, мудрость науки и красоту.
Действительно, симметрию мы можем наблюдать везде. Она противостоит хаосу, беспорядку. Значит, симметрия –
гармония и красота,
равновесие,
устойчивость.
Заключение
Человеческие представления о красивом формируются под влиянием того, что человек видит в живой природе. В различных своих творениях, очень далёких друг от друга, она может использовать одни и те же принципы. И человек в живописи, скульптуре, архитектуре, музыке применяет эти же принципы. Основополагающими принципами красоты при этом являются пропорции (в частности «золотая пропорция») и симметрия.
Трудно найти человека, который не имел бы какого-либо представления о симметрии, которая объясняет наличие определенного порядка, закономерность в расположении частей чего-либо.
Ясно, что в целом скрыт дивный
Могучий закон.
Стройным красивым колечком
Становятся листья-малютки
Или в числе небольшом,
Или без счету вокруг
Внешние чашечкой станут,
Цветочную ось окруживши
Внутренний ряд лепестков венчик
Роскошный родит.
Ныне блистает растение
Полной своей красотою.
Члены за членами в нем
Стройном порядке идут,
Сочными листьями стебель покрыт
И пышно качаясь
Дивно-прекрасный цветок
Гордо венчает его.
Гёте.
А собственно, как бы нам жилось без симметрии?
Точнее, какую роль играет симметрия в нашем мире? Неужели она лишь украшает его?
Оказывается, что без симметрии наш мир выглядел бы совсем по-другому. Ведь это именно на симметрии основаны многие законы сохранения. Например, законы сохранения энергии, импульса и момента импульса являются следствиями пространственно-временных симметрий, которые являются, как математическими, так и физическими симметриями. И без этих симметрий не было бы законов сохранений, которые во многом управляют нашим миром.
Так что симметрия – пожалуй, чуть ли не самая главная вещь во Вселенной.
Список использованной литературы:
http://wikikurgan.orbitel.ru
http://www.schoolbase.ru/
http://irinmorozova.narod.ru/best.htm ,
http://www.milogiya2007.ru/simmetr01.htm
http://fio.ifmo.ru/archive/group19/c1wu9/str01a.htm
sundekor.ru
СИММЕТРИЯ
СИММЕТРИЯ
Калдарбек Б. 1Канторе М.А. 1Канторе Т.А. 1Канторе Н.А. 11
Карымбаева С. 1Бугыбаева Г. 11
Текст работы размещён без изображений и формул.Полная версия работы доступна во вкладке "Файлы работы" в формате PDF
В природе очень многие вещи симметричны. Мы невольно отмечаем про себя необычный закат, удивительные листья растений, цветы, строгие формы кристаллов. Когда мы рассказываем об увиденном, то мысленно все созерцаем. Постепенно формируется картина окружающего нас мира, мы находим общее в различных предметах.Зеркально симметричным считается объект, состоящий из двух половин, которые являются зеркальными двойниками по отношению друг к другу.
Рисунок – 1.
Рисунок - 2. Зеркальная симметрия
Когда мы смотрим в зеркало, мы наблюдаем в нем свое отражение - это пример "зеркальной" симметрии. Зеркальное отражение - это пример так называемого "ортогонального" преобразования, изменяющего ориентацию.
Например: лист клевера или с дуба различны по форме, но их объединяет что-то общее. Эти листья имеют осевую симметрию . Симметричны не только листья растений, но и их цветы. Причем цветы могут иметь не одну ось симметрии. Два и десяти цветов не симметричны.
Симметрия присутствует и в мире животных. Бабочка имеет осевую симметрию, так же как и пчела, комар, и другие насекомые.
Исследования ученых показывают, что симметричные особи животных развиваются только в благоприятных условиях. А все случаи асимметрии обычно связаны с нарушениями развития, которые вызваны вредными воздействиями и другими стрессовыми обстоятельствами.
Рисунок 3. Осевая симметрия бабочки
Рисунок 4. Осевая симметрия кувшинки
Рисунок 5. Осевая симметрия листа
Симметрия всегда присутствует в строительстве. Ведь так проще рассчитать нагрузку на фундамент и сделать постройку прочной. В строительстве, в основном, наблюдается осевая симметрия. В любой стране есть дома они тоже симметричны. Три из десяти построек не симметричны.
Фото 1. Юрта
Фото 2. Монумент Ордабасы
Одним из самых наглядных использовании законов симметрии в жизни служат строения архитектуры. Это то, что чаще всего мы можем увидеть в архитектуре, оси симметрии используются как средства выражения архитектурного замысла. Примеров использования симметрии в архитектуре множество, одним из них является прекрасный монумент Ордабасы.
Фото 3. Каменная Юрта
Фото 4. Тайқазан.
РЕЗЮМЕ
В этой работе «Симметрия — символ красоты, гармонии и совершенства» изучены законы симметрии. Для исследований взято несколько объектов это: зеркальная симметрия, симметрия в живой природе, симметрия в архитектуре, симметрия в Выдвинутая в начале работы гипотеза подтверждается исследовательской работой.
Summary
In this work « Symmetry — a symbol of beauty, harmony and perfection »
Laws of symmetry are studied. For researches some objects it are taken: mirror symmetry, symmetry in wildlife, symmetry in architecture, symmetry in Russian national ornament. Put forward in the beginning of work the hypothesis proves to be true research work.
Литература
1. Волошинов А.В Математика и искусство.-М.: Просвещение 1992г.
2. Глейзер Г.Д.Геометрия.-12-тое изд.,-М.: Провещение 1992г.
3. Константиновна И.Г. Искусство Алтая.-М.: Просвещение 1989г.
4. А.А.Коринфский ."Народная Русь", стр. 352, Смоленск,"Русич", 1995г.
5."Математика в школе", №6, 2007г.
6. Е.Ольшанов. "Геометрия вышивки", "Наука и жизнь", №3,1995г.
7. Гончарова С.Г., Кукин Г.П. Конструктор «В мире симметрии» Математика в школе. 1996г
8. О. Иванова. Этот симметричный мир. - Первое сентября. – 2006 № 6.
9. Универсальный Справочник Школьника 5-11 классы(2005 год выпуска)
10. 1) Азевич А.И. Двадцать уроков гармонии - Москва, изд-во «Школа-Пресс», 1998 год.
11) Ведов В. Пирамиды здоровья. – Санкт-Петербург, издательство «Весь» - добрые вести, 2000 год.
12) Урманцев Ю.А. Симметрия природы и природа симметрии — М.: Мысль, 1994г.
13). Гильде В. Зеркальный мир. — М.: Мир, 1982г.
14). Современный словарь иностранных слов. — М.: Русский язык, 1993г.
15. Туганбаев М.Л., Беркут А.К., Нурматова Ж.К., Алдешов С.Е. Компьютерные цвета. Шымкент, 2011. –С.145-146.
16. Туганбаев М.Л., Беркут А.К., Нурматова Ж.К., Алдешов С.Е. Компьютерная графика. Шымкент, 2012. –С.145-146.
17.Савельева С.В., Беркут А.Х., Э.Б.Абдрахманова. Цвет. Шымкент, ЮКГУ.2010. –С.7-9.
Просмотров работы: 109
school-science.ru
Шпаргалка - Симметрия - это красота и гармония
Верхнетоемская средняя школа
Симметрия – это красота и гармония
2010 год
Содержание
Введение
Симметрия в природе
Симметрия в архитектуре
Симметрия в человеке
Заключение
Используемая литература
Введение
Цель заключается главным образом в открытие более интересного взгляда на применение математики в различных аспектах нашей жизни. Симметрия отражается не только в математических науках, но и в сфере изящных видов искусств.
Она является фундаментальным свойством природы, представление о котором имели великие мыслители разных поколений.
Мы считаем, что симметрия — это общенаучная философская категория, характеризующая структуру организации систем.
Поставив перед собой задачу раскрыть значение симметрии в построении окружающего мира, мы обратились к терминам красота и гармония. Красота неразрывно связана с симметрией. Она выражает высшую целесообразность устройства мира, подтверждает универсальность математических закономерностей, которые действуют одинаково эффективно в кристаллах и живых организмах, в произведениях искусства и в научных открытиях. Понятие симметрии проходит через всю многовековую историю человеческого творчества. Оно встречается уже у истоков человеческого знания; его широко используют все, без исключения, направления современной науки. Принципы симметрии играют важную роль в биологии и химии, физике и математике, живописи и скульптуре, поэзии и музыке. Что же такое симметрия? Какой глубокий смысл заложен в этом понятии? Почему симметрия буквально пронизывает весь окружающий нас мир?
Симметрия является фундаментальным свойством природы, представление о котором слагалось в течение десятков, сотен, тысяч поколений. В древности слово «симметрия» употреблялось в значении «гармония», «красота». Действительно, в переводе с греческого это слово означает «соразмерность, пропорциональность, одинаковость в расположении частей ».
Симметрия в природе
Симметрией обладают объекты и явления живой природы. Она не только радует глаз и вдохновляет поэтов всех времен и народов, а позволяет живым организмам лучше приспособиться к среде обитания и просто выжить. В живой природе огромное большинство живых организмов обнаруживает различные виды симметрий (формы, подобия, относительного расположения). Причем организмы разного анатомического строения могут иметь один и тот же тип внешней симметрии.
Если посмотреть на кленовый лист, снежинку, бабочку. Их объединяет то, что они симметричны. Если поставить зеркальце вдоль прочерченной на каждом рисунке прямой, то отраженная на зеркале половинка фигуры дополнит ее до целой. Потому такая симметрия называется зеркальной (осевой). Прямая, вдоль которой поставлено зеркало, называется осью симметрии. Если симметричную фигуру сложить пополам вдоль оси симметрии, то ее части совпадут.
Дальнейшие наши поиски были сосредоточены на центральной симметрии. Она наиболее характерна для цветов и плодов растений. Центральная симметрия характерна для различных плодов, но мы остановились на ягодах: голубика, черника, вишня, клюква. Рассмотрим разрез любой из этих ягод. В разрезе она представляет собой окружность, а окружность, как нам известно, имеет центр симметрии. Центральную симметрию можно наблюдать на изображении следующих цветов: цветок одуванчика, цветок мать-и-мачехи, цветок кувшинки, сердцевина ромашки, а в некоторых случаях центральной симметрией обладает и изображение всего цветка ромашки.
Не только симметричные формы окружают нас повсюду, но и сами биологические и физические законы пронизаны общим для всех них принципом симметрии. Из области кристаллографии, физики твёрдого тела он вошёл в область химии, в область молекулярных процессов, в физику атома.
/>/>
Симметрия в архитектуре
/>/>
/>
С симметрией мы встречаемся в искусстве, архитектуре, технике, быту.
Симметрия в человеке
/>
У каждого, разумеется, обнаружится родинка, прядь волос или какая-нибудь другая деталь, нарушающая внешнюю симметрию. Левый глаз никогда не бывает в точности таким, как правый, да и уголки рта находятся на разной высоте, во всяком случае у большинства людей. И все же это лишь мелкие несоответствия. Никто не усомнится, что внешне человек построен симметрично: левой руке всегда соответствует правая и обе руки совершенно одинаковы! НО! Здесь стоит остановиться. Если бы наши руки и в самом деле были совершенно одинаковы, мы могли бы в любой момент поменять их. Было бы возможно, скажем, путем трансплантации пересадить левую ладонь на правую руку, или, проще, левая перчатка подходила бы тогда к правой руке, но на самом деле это не так. Каждому известно, что сходство между нашими руками, ушами, глазами и другими частями тела такое же, как между предметом и его отражением в зеркале. Среди врачей существует мнение, что одной из причин болезней является нарушение конструкции тела. «Симметричные» животные живут дольше, чем «несимметричные». Симметрия — это показатель здоровья! Асимметрия лица — это показатель старения.
Поговорим о супермодели
Свой успех модель объясняет идеальной симметрией некоторых черт своего лица.
Пропорция и симметрия всегда необходима для нашего зрительного восприятия, чтобы считать объект красивым.
/>Сделаем вывод про человека:
Человеческое тело, так же как и тело других позвоночных, в основе своей построено зеркально симметрично.
Заключение
Не только симметричные формы окружают нас повсюду, но и сами многообразные физические и биологические законы гравитации, электричества и магнетизма, ядерных взаимодействий, наследственности пронизаны общим для всех них принципом симметрии. Симметрия проявляется в многообразных структурах и явлениях неорганического мира и живой природы. Симметрия, проявляясь в самых различных объектах материального мира, несомненно, отражает наиболее общие, наиболее фундаментальные его свойства. Поэтому исследование симметрии разнообразных природных объектов и сопоставление его результатов является удобным и надежным инструментом познания основных закономерностей существования материи.
Единство науки и искусства – важнейший залог последующего развития культуры.
Она противостоит хаосу, беспорядку. Она присутствует в нашей жизни буквально во всём, но мы настолько к ней привыкли, что не замечаем этого. Но как бы мы к ней не относились, она есть в нашей жизни буквально во всём, добавляя в неё мир, спокойствие и состояние чего-то нечуждого глазу.
Используемая литература
Универсальный Справочник Школьника 5-11 классы(2005 год выпуска)
wiki.pskovedu.ru/.../
www.dak.in.ua/.../osevaya-simmetriya-prezentaciya-3863/
www.scribd.com/doc/2622190/
www.rusedu.ru/detail_5686.html
dic.academic.ru/dic.nsf/eng.../
festival.1september.ru/articles/210924/?
www.scribd.com/doc/2622190/
www.astrosurf.com/luxorion/leonard-vinci.htm
web.mac.com/iowariver/Walking_in_Beauty/The_Red_Dragon.html
Ссылки (links): www.dak.in.ua/.../osevaya-simmetriya-prezentaciya-3863/www.scribd.com/doc/2622190/www.rusedu.ru/detail_5686.htmlwww.astrosurf.com/luxorion/leonard-vinci.htmweb.mac.com/iowariver/Walking_in_Beauty/The_Red_Dragon.htmlwww.ronl.ru
Внеурочное занятие "Симметрия в живой и неживой природе"
Разделы: Математика, Информатика
Учебный предмет: внеурочная деятельность
Класс: 6 класс
Форма занятия: комбинированное занятие
Цели занятия: развить интерес к наукам, показать взаимосвязь между математикой и окружающим миром, развитие пространственного воображения, умения мыслить и делать умозаключения, применять свои знания на практике.
Ход занятия
1. Организационный момент (1 мин)
Здравствуйте, ребята! Сегодня у нас необычное занятие. Во-первых, на нашем уроке присутствуют гости. Уважаемые гости, мы рады приветствовать вас. Во-вторых, сегодняшний интегрированное занятие по математике и информатики, мы проведём вдвоем с Мариной Александровной.
Повернитесь лицом друг к другу, улыбнитесь, мысленно друг другу хорошего настроения и успехов на уроке. Садитесь.
2. Постановка целей и задач урока (3 мин)
Ребята, сегодня мы с вами поговорим об одном из красивейших математических понятий. О каком именно, вы узнаете, просмотрев небольшой видеоролик. В процессе просмотра попробуйте ответить на вопрос: «Что объединяет все фотографии данного видеоряда?»
Промотр видео «Симметрия в живой и неживой природе» (Приложение 1)- Что общего у этих фотографий?
Предполагаемые ответы.
- Как вы думаете, о чем мы будем говорить сегодня на занятии? (о симметрии).
- Где мы можем встретить симметрию? (в жизни, в природе)
Давайте попробуем сформулировать тему нашего занятия, как бы вы её назвали? (симметрия в живой и неживой природе).(Приложение 2)
Действительно, окружающий нас мир прекрасен, потому что всё в нём создано в соответствии со строгими пропорциями, отличается соразмерностью и симметрией.
Куда мы не посмотрим, повсюду замечаем симметрию. Растения, животные, человек – всё создано по строгим законам природы. Человек давно это заметил, изучил и начал созидать, подчиняясь этим законам. Человек использовал симметрию в архитектуре. Древним храмам, башням средневековых замков, современным зданиям она придает гармоничность, законченность. С симметрией встречаем везде – в природе, технике, искусстве, подавляющее большинство самых необходимых для нас предметов — от ложки, чайника и молотка до газовой плиты, холодильника и пылесоса — обладает симметрией. Симметрия буквально пронизывает весь окружающий нас мир. Земля вполне могла бы быть названа царством симметрии…
И не зря симметрия изначально употреблялась в словах гармония и красота.
3. Актуализация знаний (3 мин)
Ребята, мы увидели, как много окружающих нас понятий тесно взаимосвязаны с понятием симметрии. И мы уже кое-что о ней знаем. На прошлом занятии мы с вами изучали понятие симметрии, рассматривали виды симметрии, строили симметричные геометрические фигуры. Давайте вспомним эти сведения и попробуем ответить на несколько вопросов.
– Какой из этих рисунков обладает симметрией, а какой нет?
– Почему вы так решили? Как бы вы описали словами первый рисунок?
Ответы: – Первый обладает.
– Он более правильный. (Симметрия – это правильность)
– Какой из этих рисунков вы считаете более законченным, а какой хочется дорисовать?
Ответ:
– Первый закончен. (Симметрия – это завершенность)
– Какой из этих бабочек проще летать? (той, у которой крылышки здоровы, или у которой крыло раненое)
– Какой из этих пейзажей создает атмосферу умиротворенности?
Ответ
– Первый. (Симметрия – это спокойствие)
– А как одним словом можно назвать равновесие, спокойствие, завершенность и правильность?
Ответ
– Красота или гармония.
Хочется вспомнить слова древнегреческого философа Платона: "...быть прекрасным значит быть симметричным и соразмерным".
А теперь используя все свои знания, дайте мне четкое определение симметрии.
(Симметрия – это соразмерное, пропорциональное расположение частей чего-либо по отношению к центру, прямой или плоскости)
Молодцы, ребята!
4. Применение знаний в новой ситуации (15 мин)
У каждого на столе лежит карточка, на которой расположены симметричные и несимметричные картинки. Ваша задача, указать стрелочкой, в какую колонку вы отнесете данные обекты. Работать вы будете в парах. На выполнение задания отводится минута. (Приложение 3)
А теперь мы с вами проверим, как вы выполнили это задание.
Задание на проектной доске (см. используемую литературу)
- А с какими видами симметрии мы познакомились на прошлом занятии?
- Какая симметрия называется осевой?
На доске задание…..
- Скажите, как определить на каком расстоянии от оси симметрии мы должны распределить симметричный объект?
Молодцы, вы справились с этим заданием.
- Наверно каждый из вас уже раньше создавали симметричные объекты?
- Постарайтесь вспомнить, когда?
- Какой праздник у нас впереди?
- Чем украшаем мы комнату, окна? (предполагаемые ответы)
Сегодня мы тоже будем моделировать симметричные объекты. Для того, чтобы определить объект моделирования отгадаем загадку:
Шевелилась у цветкаВсе четыре лепестка,Я сорвать его хотел – Он вспорхнул и улетел.(бабочка)
- Посмотрите на бабочку
- Из каких частей она состоит? (голова, туловище, крылья)
- Что можно сказать о её крыльях? (они одинаковы с противоположных сторон)
- Можно ли сказать, что у бабочки крылья симметричны относительно прямой? (да)
- Докажите это, используя бабочку из бумаги.
- Симметричный рисунок можно согнуть относительно одной оси симметрии.
- Где эта ось у бабочки? Покажите.
- Молодцы!
- Ребята, а мне интересно, можно ли в графическом редакторе сделать вот такую бабочку? (Слайд)
- Как вы считаете?
- Если можно, то как?
- Что достаточно изобразить, чтобы нарисовать бабочку?
- Из каких геометрических фигур состоит бабочка?
- Какие инструменты нам с вами понадобятся?
- как выделить фрагмент? (открыть свёрнутый до урока Paint и там продемонстрировать)
- как скопировать изображение?
- как вставить изображение?
- как позаботиться о сохранении рисунка?
- Как изменить размеры изображения?
5. Практическая работа (20 мин)
- А сейчас мы научимся создавать симметричный рисунок в графическом редакторе Paint.
- Но сначала познакомимся с алгоритмом создания симметричных рисунков. (Приложение 3)
- Откройте в папке «Информатика» текстовый документ «Создание симметричных рисунков»
- Прочитайте про себя.
- Приступайте к работе. Кому нужна моя помощь – поднимите руку.
- Чтобы закончить нашу работу, посмотрите на фотографии бабочек.
- Обратите внимание на симметричный рисунок на крыльях бабочек и на их цвет.
- Украшайте своих бабочек.
- Сохраните свои работы.
- Откройте ГР Paint известным способом. Инструкция на листах: Для получения симметричного изображения необходимо:
|
– А сейчас вы попробуете самостоятельно нарисовать свою бабочку, исользуя симметрию.
- Украсьте крылья узорами, “нарядите” бабочку в красивое, яркое, узорчатое платье.
- Сохраните свою бабочку в сетевом диске под своей фамилией.
- На работу вам отводится 7 минут.
6. Рефлексия (3 мин)
– Ребята, спасибо вам за работу! Без помощи и поддержке друг друга мы не смогли бы достичь цели. Я очень довольна вашей работой на уроке. Считаете ли вы, что мы не напрасно провели эти минуты вместе?
Мы с вами увидели, что симметрия - неотъемлемая, можно сказать, обязательная часть нашей жизни.
Так, давайте ребята, ценить красоту, любить красоту и восхищаться красотой природы с ее удивительной симметрией!!!
Дотронуться хотела я рукамиДо самого красивого цветка.А он, взмахнув своими лепестками,Вспорхнул и улетел под облака!
- Ребята, кому наше занятие понравилось, нарисуйте солнышко.
- У кого остались недопонимания, сомнения, нарисуйте тучку.
- Если занятие не понравилось, нарисуйте красный круг.
Используемая литература и интернет-ресурсы
- ttp://school-collection.edu.ru
- http://festival.1september.ru/articles/632940/
xn--i1abbnckbmcl9fb.xn--p1ai
Презентация «Симметрия»
Слайды и текст этой презентации
Слайд 1

CимметрияСимметрия – это идея, с помощью которой человек веками пытался объяснить и создать порядок, красоту и совершенство. Г. Вейль
Слайд 2

Содержание. Введение Симметрия в растениях. Симметрия в мире насекомых, рыб, птиц, животных. Симметрия в неживой природе. Симметрия в архитектуре, скульптуре. Музыка и симметрия. Литература и симметрия.
Слайд 3

Понятие симметрии проходит через всю многовековую историю человеческого творчества. Оно встречается уже у истоков человеческого знания, его широко используют все без исключения направления современной науки. Принципы симметрии играют важную роль в физике и математике, химии и биологии, физике и архитектуре, живописи и скульптуре, поэзии и музыке. Законы природы, управляющие неисчерпаемой в своём многообразии картиной явлений, в свою очередь, подчиняются принципам симметрии.
Слайд 4

Симметрия в живой природе. Внимательное наблюдение обнаруживает, что основу красоты многих форм, созданных природой, составляет симметрия, точнее все ее виды – от простейших до самых сложных. В основе строения любой живой формы принцип симметрии. Когда мы хотим нарисовать лист растения или бабочку, то нам приходится учитывать их осевую симметрию. Средняя жилка для листа и туловище для бабочки служит осью симметрии. Ярко выраженной симметрией обладают листья, ветви, цветы, плоды.
Слайд 5

Симметрия в растениях.
Слайд 6

Слайд 7

Симметрия в живой природе.Симметрия встречается и в животном мире. Однако в отличие от мира растений симметрия в животном мире наблюдается не так часто. Можно сказать, что каждое животное состоит из правой и левой половин. Например, правое и левое ухо, правый и левый глаз, правый и левый рог и т. д.
Слайд 8

Симметрия в мире насекомых.
Слайд 9

Слайд 10

Слайд 11

Слайд 12

Слайд 13

Симметрия в мире рыб.
Слайд 14

Слайд 15

Слайд 16

Симметрия в мире птиц.
Слайд 17

Слайд 18

Симметрия в мире животных.
Слайд 19

Слайд 20

Слайд 21

Симметрия в неживой природе.Воздействие на облик земной поверхности таких природных факторов, как ветер, вода, солнечный свет, весьма стихийно и часто носит беспорядочный характер. Однако песчаные дюны, галька на морском берегу, кратер потухшего вулкана имеют, как правило, геометрически правильные формы. Именно кристаллы вносят в мир неживой природы очарование симметрии. Он сыплет с неба мелкой крупой, летает вокруг фонарей огромными пушистыми хлопьями, стоит столбом в лунном свете ледяными иглами. Казалось бы, какая ерунда! Всего-то замёрзшая вода. Но сколько вопросов возникает у человека, глядящего на снежинки. Раньше снежинки рассматривали исключительно как один из вариантов кристаллизированного вещества. Учёные задались вопросом о том, почему они все разные и в то же время симметричные. В итоге выяснилось, что снежинка – это группа кристалликов, образованная более чем из двухсот ледяных частичек.
Слайд 22

Слайд 23

Слайд 24

Слайд 25

Слайд 26

Симметрия в архитектуре, скульптуре. Человеческое творчество во всех своих проявлениях тяготеет к симметрии. На этот счёт хорошо высказался известный французский архитектор Ле Корбюзье, в своей книге «Архитектура XX века» он писал: «Человеку необходим порядок: без него все его действия теряют согласованность, логическую взаимность. Чем совершеннее порядок, тем спокойнее и увереннее чувствует себя человек. Он делает умозрительные построения, основываясь на порядок, который продиктован ему потребностями его психики, это творческий процесс. Творчество есть акт упорядочения». Нагляднее всего видна симметрия в архитектуре. Особенно блистательно использовали симметрию в архитектурных сооружениях древние зодчие. Причём древнегреческие архитекторы были убеждены, что в своих произведениях они руководствуются законами, которые управляют природой. В сознании древних греков симметрия стала олицетворением закономерности, целесообразности, красоты.
Слайд 27

Слайд 28

Слайд 29

Слайд 30

Музыка и симметрия.Симметрия часто используется и в других видах искусства. В том числе в музыке. Ряд музыкальных форм строится симметрично.
Слайд 31

Литература и симметрия. В литературных произведениях существует симметрия образов, положений, мышления. Вспомним хотя бы закон возмездия в греческой трагедии, где виновный становится жертвой такого же преступления. В русском языке есть «симметричные слова – палиндромы, которые можно читать одинаково в двух направлениях: Шалаш, казак, радар, Алла, Анна, кок, поп.
Слайд 32

Спасибо за внимание!
lusana.ru
Красота, симметрия и сверхстимулы. Эволюция человека. Книга 1. Обезьяны, кости и гены
Красота, симметрия и сверхстимулы
Почему одни вещи кажутся нам красивыми (то есть при взгляде на них нейроны мозга выделяют эндорфины и мы испытываем удовольствие), а другие нет?
Свойственное людям «чувство прекрасного» — сложное явление, складывающееся из нескольких разнородных элементов. С красотой человеческого тела все более или менее понятно: как правило, мы считаем красивыми в людях такие внешние признаки, которые свидетельствуют о высоком «качестве генов» и позволяют предположить, что у этого человека будет здоровое, крепкое потомство. Люди, которым не нравились такие признаки, у которых не выделялись эндорфины при взгляде на них, выбирали себе неудачных брачных партнеров. В результате гены «эстетической тупости», «непонимания красоты» и «безвкусицы» отсеивались отбором. Тема эстетических предпочтений при выборе брачного партнера подробно раскрыта в книге М. Л. Бутовской «Тайны пола» (2004).
Нет ничего удивительного в том, что нам может нравиться отдельный признак в отрыве от целого. Наш мозг не сразу собирает целостный образ из сигналов, приходящих от глаз в затылочные доли мозга. Сначала он выделяет в этих сигналах именно отдельные признаки: вертикальные и горизонтальные контуры, движение, новизну. Лишь потом из всего этого собирается цельная картинка — модель реальности, которая опять-таки может анализироваться и оцениваться по частям (подробнее см. в книге К. Фрита «Мозг и душа»).
Одним из надежных «индикаторов приспособленности» человека и других животных является симметричность. Чем симметричнее лицо и тело, тем, как правило, крепче здоровье индивида и меньше вредных мутаций в его генах. Многочисленные эксперименты показали, что симметрия лица и тела — важнейший фактор, влияющий на оценку красоты и сексуальной привлекательности. Чем симметричнее лицо, тем оно кажется нам красивее. Возможно, поэтому нас привлекают и кажутся красивыми симметричные предметы, особенно если эта симметрия достаточно изощренна и чуть-чуть несовершенна, как, например, у снежинок. Стоит ли удивляться, что симметрия стала одним из основополагающих мотивов изобразительного искусства.
Любовь к симметрии, похоже, зародилась очень давно. На эту мысль наводит форма ашельских рубил — бифасов. Зачем наши предки тратили столько лишних усилий, придавая своим каменным ножам такие правильные, симметричные очертания? Это трудно объяснить функциональностью. Ножу не обязательно быть симметричным, чтобы успешно справляться со своими функциями. Нож — он и есть нож, был бы острый кончик да режущий край. Бифасы по своей форме немного напоминают клыки хищников — не они ли и послужили прообразом? Но клыки обычно изогнуты, а бифасы прямые; по-видимому, мастера пытались придать им правильную двустороннюю симметрию. Некоторые эксперты предполагают, что совершенство формы рубила могло служить чем-то вроде «индикатора приспособленности» для эректусов и гейдельбержцев, и даже поддерживаться половым отбором.
Еще одна эволюционная концепция, помогающая понять природу чувства прекрасного, — это идея «сенсорного смещения», или «сенсорного драйва». В ходе эволюции отбор подстраивает сенсорное восприятие животных под нужды выживания. Органы чувств и отделы мозга, занятые анализом поступающих от этих органов сигналов, настраиваются так, чтобы быстрее выделять информацию, значимую для выживания и размножения. Сенсорное восприятие не может быть абсолютно объективным и неизбирательным: это было бы крайне неэффективно и расточительно.
Любое животное реагирует на одни стимулы острее, чем на другие. «Энергичность реакции» основана на мотивации, а мотивация у животных неотделима от эмоций. Если мы хотим манипулировать эмоциями какого-нибудь животного (например, человека), следует предъявлять ему такие стимулы, на которые его мозг в ходе эволюции приспособился реагировать наиболее бурно. Этим «пользуются», например, некоторые рыбы-цихлиды африканских озер: самцы этих видов в ходе эволюции окрашиваются в такие цвета, которые лучше всего воспринимаются фоторецепторами (светочувствительными клетками сетчатки) данного вида рыб, а цветовое восприятие цихлид подстраивается к глубине обитания, прозрачности воды и диете. Другой пример, про бабочек и цветы, упомянут в книге «Рождение сложности»: возможно, крылья дневных бабочек окрашены столь ярко, потому что глаза их потенциальных брачных партнеров миллионы лет приспосабливались высматривать яркие цветы — источники нектара.
Часто максимального эффекта удается достичь, предъявив стимул, преувеличенный по сравнению с реальностью, — так называемый сверхстимул.
Вы легко поймете, что такое «сенсорное смещение» и «сверхстимул», если иногда собираете ягоды в лесу. Попробуйте после целого дня, проведенного за сбором брусники, закрыть глаза — какой образ тотчас предстанет перед вашим мысленным взором? Не знаю, как вы, а я в такой ситуации всегда вижу самый обсыпной, самый великолепный ягодный куст с такими крупными и яркими ягодами, каких и в природе-то не бывает. Это идеальный образ моей цели — того, что напряженно выискивали мои глаза целый день. С этим образом мой мозг сравнивал реальные кусты, оценивая степень их соответствия образу, чтобы решить, стоит ли нагибаться. И он кажется таким реальным, таким настоящим, что психологические корни идеализма перестают выглядеть такими уж непонятными. Следующий вопрос: если бы вы хотели произвести на меня в этот момент самое сильное впечатление, какой стимул следовало бы мне предъявить? Я думаю, что «сверхкуст со сверхъягодами», настоящий или нарисованный, подошел бы в самый раз.
Преувеличенные черты женственности у «палеолитических венер» — это, конечно, сверхстимулы. При взгляде на них у палеолитических мужчин выделялись эндорфины, окситоцин и прочие гормоны (см. главу «Генетика души», кн. 2). Самцам было приятно, и социальный статус художника рос как на дрожжах. Эти черты могли играть и какую-то другую роль — символизировать плодородие, например — но быть сверхстимулами они от этого не переставали.
К числу значимых могут относиться самые разные сигналы. В том числе несущие информацию о чем-то новом, необычном. Что ж, и это проявляется в нашем искусстве. Художники из кожи вон лезут, стараясь удивить зрителей, преподнести им что-то неожиданное. Это приводит к выделению эндорфинов в мозге зрителей, и они говорят: «Ах, какой художник!», повышая тем самым репутацию и социальный статус творца.
Эндорфины выделяются и при стрессе, и при легком испуге. Может быть, поэтому палеолитическим художникам казались прекрасными (да и нам кажутся) не только крупные травоядные животные — потенциальная добыча, напоминание о волнительных сценах охоты, — но и силуэты опасных хищников.
Поделитесь на страничкеСледующая глава >
bio.wikireading.ru