Работа № 10 Ломаные линии и сплайновые кривые. Кривая и ломаная линия

Что такое ломаная?

В геометрии часто можно встретить такое понятие, как «ломаная». Поэтому мы решили подробно рассказать вам о том, что такое ломаная, и о ее составляющих. Начнем с общего определения, а потом опишем отдельные элементы ломаной линии - звенья, вершины. И, конечно, вы узнаете, чем ломаная отличается от прямой и кривой линий не только визуально, но и, разумеется, с геометрической точки зрения.

Что такое ломаная линия

Ломаной линией называется геометрическая фигура, представляющая собой непрямую линию, которая состоит из последовательно соединенных между собой отрезков. Отрезки эти могут соединяться под совершенно разными углами и даже пересекаться, однако они не должны выстраиваться в прямую линию. Строго говоря, если есть хотя бы небольшой, даже едва заметный угол между соединяемыми отрезками, то это уже будет ломаная линия. Этим ломаная линия отличается от прямой. Прямая также может состоять из отрезков, однако угол соединения этих отрезков должен быть равен нулю, иначе речь будет идти уже о ломаной линии. Что касается отличия ломаной от кривой, то здесь также все очень просто — отрезки ломаной представляют собой прямую линию, а отрезки кривой — нет.

Типы ломаных

Ломаные могут строиться по-разному: так, существуют замкнутые и незамкнутые ломаные, самопересекающиеся и непересекающиеся. Замкнутая ломаная представляет собой определенную фигуру — многоугольник. Самопересекающейся называется такая ломаная линия, отрезки которой имеют пересечения. Хорошие примеры различных ломаных с комментариями можно найти тут. Также подробное представление о различных типах ломаных дано здесь. Как вы уже, наверное, догадались, ломаные могут быть четырех типов по своей структуре:

незамкнутые без пересечений;
замкнутые без пересечений;
незамкнутые самопересекающиеся;
замкнутые самопересекающиеся.

Теперь расскажем о том, что такое звено ломаной. Зв

elhow.ru

звенья, вершины и длина, разновидности

Ломаной называется особая разновидность геометрической фигуры, которая составлена из нескольких отрезков. Эти отрезки последовательно соединены между собой своими концами. Конец каждого отрезка, за исключением последнего, является начальной точкой следующего. Смежные отрезки не должны находиться на одной прямой линии.

Существует и другое определение того, что такое ломаная фигура. Согласно ему это геометрический объект, который представляет собой непрямую линию и состоит из череды отрезков, последовательно соединенных между собой. Эти отрезки могут образовывать углы различной величины. Даже если угол между ними будет минимальным, он все равно будет ломать линию и ее уже можно считать ломаной. В этом и заключается ее основное отличие от прямой.

Это интересно: разность чисел – что это, как ее найти?

Ломаную линию следует отличать от кривой. Основное отличие заключается в том, что отрезки ломаной являются прямыми линиями, а отрезки кривой — нет. Эти понятия подробно объяснит школьная программа по математике за 8 класс.

Звенья, вершины и длина

Чтобы полностью усвоить сущность и свойства этого понятия, рассмотрим, что такое звенья ломаной линии в математике, а также что представляют собой ее вершины и длина:

Отдельные отрезки, составляющие такую линию, называются ее звеньями. Каждая такая линия может состоять как минимум из двух звеньев. Максимальное количество звеньев при этом не ограничено.
Точки соединения концов этих отрезков называются вершинами.
Если концы ломаной соединяются в одной точке, такая фигура носит название замкнутой. Ее звенья могут иметь взаимные пересечения.
Если же звенья одной замкнутой линии не пересекаются между собой, она называется многоугольником.
Геометрическое понятие длины ломаной включает в себя сумму длин всех ее звеньев.

Интересно знать: что такое выпуклый четырехугольник, его особенности и признаки.

Обозначение ее составляется из заглавных латинских букв, которые стоят на вершинах:

Каждая вершина на рисунке обозначается одной буквой (например: A, B, C, D или E).
Звено принято обозначать двумя буквами (концы соответствующего отрезка, например: AB, BC, CD, DE).

В целом такую совокупность принято называть ABCDE или EDCBA.

Обратите внимание: что такое луч в геометрии.

Разновидности

В геометрии принято различать несколько разновидностей по структуре:

Замкнутые самопересекающиеся.
Незамкнутые самопересекающиеся.
Замкнутые без самопересечений.
Незамкнутые без самопересечений.

Как уже было описано выше, замкнутая непересекающаяся фигура получила название многоугольника.

Если звенья фигуры имеют пересечения между собой — она называется самопересекающейся.

Многоугольники

Многоугольник — это геометрическая фигура, которая характеризуется количеством углов и звеньев. Углы составлены парами звеньев замкнутой ломаной, сходящимися в одной точке. Звенья называются еще сторонами многоугольника. Общие точки двух отрезков называют вершинами многоугольника.

Количество звеньев или сторон в каждом многоугольнике соответствует количеству углов в нем же. Замкнутая ломаная из трех отрезков называется треугольником. Ломаная из четырех звеньев получила название четырехугольника. Фигура из пяти отрезков — пятиугольник и т. д.

Часть плоскости, которая ограничена замкнутой ломаной, называется плоским многоугольником. Другое ее название — многоугольная область.

Свойства

Ниже приведены основные свойства, общие для всех многоугольников:

Если вершины многоугольника служат концами одной стороны, их называют соседними. Если же вершины не прилежат к одной стороне, они несоседние.
Наименьшее количество сторон у многоугольника равняется трем. Однако треугольники, находясь рядом друг с другом, могут образовывать новые фигуры.
Если отрезок соединяет между собой несоседние вершины, он носит название диагонали.
Если фигура лежит относительно одной прямой в любой полуплоскости, она называется выпуклой. При этом прямая содержит в себе одну сторону фигуры и сама принадлежит полуплоскости.
Угол, смежный внутреннему углу многоугольника при некоторой вершине, называется внешним.
Если все стороны и углы многоугольника равны, он называется правильным.

Треугольники

Треугольником в математике принято называть плоскую геометрическую фигуру, которая состоит из трех точек, не располагающихся на одной прямой. Эти точки соединены тремя отрезками.

Точки представляют собой вершины или треугольника, а отрезки — его стороны. Возле каждой из вершин образуется угол треугольника. Таким образом эта фигура имеет три угла, что видно из ее названия.

Различают следующие виды треугольников:

Равносторонние — все стороны их равны по длине.
Разносторонние — все стороны различаются по длине.
Равнобедренные — две стороны из трех имеют одинаковую длину.
Остроугольные — если все углы острые.
Прямоугольные — если имеется прямой угол.
Тупоугольные — если есть один тупой угол.

Четырехугольники

Плоская геометрическая фигура, имеющая четыре угла и четыре стороны, называется четырехугольником.

Если все углы у четырехугольника прямые — это прямоугольник.

Правильный четырехугольник носит название квадрата.

Существуют и другие разновидности четырехугольников — ромб, трапеция, параллелограмм и пр. Все они подчиняются общим правилам, описанным выше.

obrazovanie.guru

Ломаные линии и сплайновые кривые

Работа № 9

Ломаные линии и сплайновые кривые

Цель работы: Изучение приемов работы с ломаными линиями и сплайновыми кривыми: кривая Безье, NURBS-кривая. Редактирование сплайновых кривых. Способы создания "скульптурных" поверхностей.

Введение

В предыдущих работах рассматривались трехмерные модели, образованные как простыми, так и сложными геометрическими формами.

Достаточно вспомнить моделирование тонкой пластины и корпуса лодки. Поверхности сложной формы легко получить по эскизам ломаных и кривых (сплайновых) линий.

В этой работе мы более подробно познакомимся со способами моделирования сложных ("скульптурных") поверхностей, которые впервые потребовались для создания форм новых автомобилей, самолетов, космических кораблей, многочисленных бытовых приборов.

	Первый автомобиль с паровой машиной – 1769 г.
	Автомобиль – 1896 г.
	Автомобиль фирмы Рено (Renault) – 2006 г.

В работе рассматриваются новые команды и термины, смысл которых мы будем раскрывать постепенно:

Материал для чтения

1.КомандаЛоманая – . Позволяет построить ломаную линию, состоящую из отрезков прямых.

2. Сплайновые кривые.Термин "сплайн" происходит от английского слова spline. Так называется гибкая полоска стали, при помощи которой чертежники проводили через заданные точки плавные кривые. Раньше подобный способ построения плавных обводов различных тел, таких как, например, корпус корабля, кузов автомобиля был довольно широко распространен в практике машиностроения. Сплайном называли и разметочную веревку, кривизна которой регулировалась подвешенными грузиками (рис. 9.1). В результате форма тела задавалась при помощи набора очень точно изготовленных сечений – плазов. Появление компьютеров позволило перейти от этого механического метода к более эффективному математическому способу задания поверхности обтекаемого тела.

Рис. 9.1.

Сплайн – это гладкая кривая, которая строится с использованием дуг и проходит через две или более контрольных точек, управляющих формой сплайна. Чем больше используется контрольных точек, тем кривая получается более гладкой.

В основе этого подхода к описанию поверхностей лежит использование сравнительно несложных формул, позволяющих восстанавливать облик изделия с необходимой точностью. Для большинства тел, встречающихся на практике, невозможно найти универсальную формулу, которая может описать соответствующую поверхность глобально или, как принято говорить, в целом. Вместе с тем аналитическое описание (описание посредством формул) внешних обводов изделия, то есть задание в трехмерном пространстве двумерной поверхности, должно быть достаточно экономным. Это особенно важно, когда речь идет об обработке изделий на станках с числовым программным управлением.

Два из наиболее общих типов сплайнов – кривые Безье и В-сплайны (би-сплайны). Типичным примером сплайнов являются также неоднородные рациональные NURBS-кривые ("нурбс"-кривые).

3. Кривая Безье – .В начале 70-х годов профессор Пьер Безье, проектируя на компьютере корпуса автомобилей "Рено", впервые применил для этой цели уравнения, описывающие кривые, впоследствии названные его именем.

Кривые Безье записываются в памяти компьютера в виде математических формул, поэтому рисунки, полученные с помощью этих кривых, обеспечивают возможность масштабирования без потери качества изображения

Обобщение методов Безье и B-сплайнов в начале 70-х годов позволило получить одно из мощнейших и универсальных средств геометрического моделирования криволинейных обводов − NURBS-технологию. Из-за своей гибкости и точности NURBS-модели могут использоваться в любом процессе иллюстрации, анимации и промышленного дизайна.

4. NURBS-кривая – . Сокращение (аббревиатура) NURBS обозначает Non-Uniform Rational B-Splines, то есть неравномерные рациональные B-сплайны. Это математические объекты для задания двумерных кривых и гладких поверхностей в трехмерном пространстве.

Неоднородный (Non-Uniform) означает, что различные области объектов NURBS (кривых или поверхностей) обладают различными свойствами (весами), значения которых не равны между собой.

Рациональный (Rational) означает, что объект NURBS может быть описан с помощью математических формул.

Большинство современных САПР и систем компьютерной анимации поддерживают моделирование с использованием NURBS-кривых и поверхностей;

- с помощью NURBS ‑ кривых проще имитировать поверхности природных объектов или объектов, поверхности которых имеют сложным образом искривленные профили;

- NURBS-модели обеспечивают лучшее качество визуализации закругленных краев объектов благодаря разбиению на грани, выполняемому с использованием аналитических выражений. Например, обводы корпуса автомобиля моделируются с использованием NURBS-сплайнов.

Соотношение между сплайнами различных типов качественно иллюстрируется рис. 9.2.

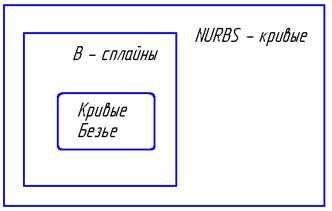
Рис. 9.2.

Задание координат характерной точки.

Активизируйте характерную точку. В Строке параметров объекта появятся поля с координатами этой точки. Введите в поля координат новые значения и зафиксируйте их, нажав клавишу Enter. После этого характерная точка займет новое положение.

Удаление характерной точки.

Активизируйте характерную точку и нажмите клавишу Delete. После этого характерная точка исчезнет, и объект перестроится в соответствии с положением оставшихся характерных точек.

Примечание.

1. При редактировании характерных точек перечисленные способы можно комбинировать. Для этого следует выбрать из объектного меню команду Редактировать точки.

2. Редактирование объекта завершается нажатием кнопки Создать объект или выбором соответствующей команды из объектного меню.

Задание 2. Редактирование построенных кривых

2.1. Редактирование ломаной линии:

1) войдите в режим редактирования ломаной линии;

2) освойте все перечисленные выше приемы редактирования характерных точек;

3) прочитайте дополнительную справку и попробуйте проделать описанные действия с характерными точками ломаной линии. Обратите внимание на происходящие изменения;

4) создайте объект.

2.2. Редактирование кривой Безье:

1) войдите в режим редактирования кривой. Обратите внимание, что у каждой вершины кривой Безье появились касательные векторы, на концах которых есть управляющие точки или маркеры (рис. 9.6).

Рис. 9.6. редактирование кривой Безье.

Вы можете:

– перемещать вершины кривой Безье;

– перемещать управляющие точки (маркеры) и поворачивать касательные векторы;

– добавлять и удалять вершины кривой Безье;

2) попробуйте проделать эти операции и обратите внимание на изменения, которые происходят с кривой Безье.

2.3. Редактирование NURBS-кривой:

1) войдите в режим редактирования NURBS-кривой (рис. 9.7).

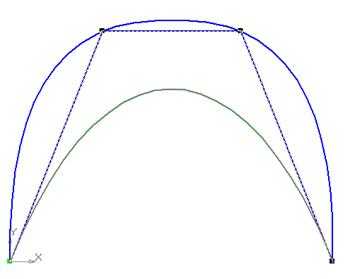
Рис. 9.7.

Панель свойств NURBS-кривой имеет вид, показанный на рис. 9.8.

Рис. 9.8. Панель свойств NURBS–кривой.

Здесь:

т − координаты выделенной (указанной) характерной точки,

Вес точки – образно говоря, сила притяжения кривой к точке;

Порядок NURBS-кривой – число, на единицу большее степени полиномов, описывающих участки, из которых состоит кривая;

Режим построения NURBS-кривой: разомкнутая/замкнутая – ;

2) попробуйте поменять параметры NURBS-кривой. Изучите влияние веса точки и порядка кривой.

Работа № 9

Ломаные линии и сплайновые кривые

Введение

	Первый автомобиль с паровой машиной – 1769 г.
	Автомобиль – 1896 г.
	Автомобиль фирмы Рено (Renault) – 2006 г.

В работе рассматриваются новые команды и термины, смысл которых мы будем раскрывать постепенно:

Материал для чтения

1.КомандаЛоманая – . Позволяет построить ломаную линию, состоящую из отрезков прямых.

Рис. 9.1.

Рациональный (Rational) означает, что объект NURBS может быть описан с помощью математических формул.

Соотношение между сплайнами различных типов качественно иллюстрируется рис. 9.2.

Рис. 9.2.

Ломаные линии, кривые линии, волнистые линии, и линии, вводящие в кадр - Композиция фото - Статьи и уроки

Кривые и волнистые линии обладают изяществом, взгляд скользит по ним легко и спокойно. Поэтому такие линии принято считать линиями легкости, нежности и красоты.

Эти линии сами по себе настолько симпатичны и приятны нашему взгляду, что способны придавать определенную привлекательность любым снимкам независимо от их содержания.

По этой причине различные кривые, дугообразные и волнистые линии желательно использовать в линейных композиционных построениях как можно чаще.

Ломаные линии, зигзаги в отличие от спокойных прямых и тем боле изящных кривых линий более динамичны и способны в ряде случаев придавать снимку беспокойный и даже взрывной характер.

Скорее всего, подобное впечатление при рассматривании таких снимков связано с частым, скачкообразным изменением направления нашего взгляда.

Зрительное и психологическое воздействие, которое производят ломаные линии, необходимо учитывать при композиционных построениях фотоснимков соответствующего содержания. В одних случаях такие линии могут помочь автору подчеркнуть тревожный характер запечатленного момента, а в других, наоборот, лишить снимок спокойного, лирического настроения.

Особая роль при линейных построениях отводится линиям, которые принято называть «вводящими в кадр». Это реальные или воображаемые линии, которые берут начало у одного из нижних углов кадра и идут в его глубину, чаще всего к смысловому центру снимка, расположенного в точке «золотого сечения».

Построенные по этому принципу снимки легко «прочитываются», их содержание почти мгновенно доходит до сознания зрителя, а это одно из главных условий хорошей композиции.

Происходит это потому, что наш взгляд легко, не задерживаясь, скользит вдоль такой линии и сразу же находит тот элемент изображения, которому отведена главенствующая роль в трактовке идеи фотоснимка.

Такое свойство «вводящих в кадр линий» дает основание считать их одними из важнейших в линейном построении любых снимков. Следует заметить, что эти линии настолько органичны и естественны, что даже очень частое их использование не вызывает у зрителей чувства штампа.

foto-mir.biz

ТОЧКА, ЛИНИЯ. ПРЯМЫЕ ЛИНИИ (ВЕРТИКАЛЬНЫЕ, ГОРИЗОНТАЛЬНЫЕ, НАКЛОННЫЕ). КРИВАЯ ЛИНИЯ. ЛОМАНАЯ ЛИНИЯ. ЗАМКНУТАЯ И НЕЗАМКНУТАЯ ЛИНИИ. ОБРАЗОВАНИЕ МНОЖЕСТВ - ПРИЗНАКИ И СВОЙСТВА ПРЕДМЕТОВ. МНОЖЕСТВА. ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ. НАТУРАЛЬНЫЕ ЧИСЛА 1-10 И ЧИСЛО 0 - Математика. 1 класс. I семестр - конспекты уроков - План урока - Конспект урока - Планы уроков

ПРИЗНАКИ И СВОЙСТВА ПРЕДМЕТОВ. МНОЖЕСТВА. ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ. НАТУРАЛЬНЫЕ ЧИСЛА 1-10 И ЧИСЛО 0

Урок 7. ТОЧКА, ЛИНИЯ. ПРЯМЫЕ ЛИНИИ (ВЕРТИКАЛЬНЫЕ, ГОРИЗОНТАЛЬНЫЕ, НАКЛОННЫЕ). КРИВАЯ ЛИНИЯ. ЛОМАНАЯ ЛИНИЯ. ЗАМКНУТАЯ И НЕЗАМКНУТАЯ ЛИНИИ. ОБРАЗОВАНИЕ МНОЖЕСТВ

Цель: ознакомить учащихся с составом числа 3, треугольником, его элементами; дать понятие о прямую, кривую и ломаную линии; учить чертить линии; развивать мышление; воспитывать старательность.

Ход урока

I. ОРГАНИЗАЦИОННЫЙ МОМЕНТ

II. ПОВТОРЕНИЕ ИЗУЧЕННОГО МАТЕРИАЛА

1. Веселый счет

Кошка Мурка на все ножки

Надела шелковые чулочки.

И одна где-то потерялась.

Сколько в кошке осталось?

2. Игра «Не зевай, продолжай»

— Назовите числа от 1 до 10; от 10 до 1.

3. Логические задачи

• Из-за пенька показалось 6 заячьих ушей. Один зайчик убежал. Сколько ушей теперь видно из-за пенька? Сколько там зайцев?

• В норе блестело 6 глаз. Сколько волков сидело в норе?

III. ОЗНАКОМЛЕНИЕ С НОВЫМ МАТЕРИАЛОМ.

РАБОТА ПО УЧЕБНИКУ (С. 13)

Задача 1

— На рисунке вы видите точку. Это точка-путешественница. Много точек образуют прямую. Эта линия без начала и конца. Прямые линии бывают вертикальные, горизонтальные, наклонные.

Задание 2

— Это кривая и ломаная линии.

Задание 3

— Бывают линии запертые и незапертые.

— Назовите каждую линию.

Задание 4

— Что нарисовано?

— Образуйте множества по цвету; по размеру. Сколько элементов в каждом множестве?

Задание 5

Работа в тетради

— Нарисуйте линии по образцу.

Физкультминутка

IV. ЗАКРЕПЛЕНИЕ ИЗУЧЕННОГО МАТЕРИАЛА

1. Распознавание линий на практике

Учитель бросает веревку на стол.

— Какая линия получилась? (Кривая линия)

— А сейчас девочка возьмет за один конец веревки, а мальчик — за другой конец веревки. Натяните ее.

— Какая линия получилась? {Прямая)

2. Игра «Угадай, какая линия?»

• Цветное коромысло

Через реку повисло. (Радуга. Кривая линия)

• Кто всю ночь по крыше бьет да постукивает,

Бормочет и поет, убаюкивает? (Дождь, прямые линии)

• Висит сито

Не людьми свит. (Паутину. Кривые линии)

3. Практическая работа в тетради

— Синим карандашом начертите прямую линию, а зеленым — кривую.

V. ИТОГ УРОКА. РЕФЛЕКСИЯ

— С какими линиями вы ознакомились?

— Приведите примеры таких линий.

schooled.ru

Линии - геометрия и искусство

Кандинский систематизировал свои взгляды на живопись в книге «Точка и линия на плоскости» (1926). Изучая геометрические формы, художник нашёл, что с их помощью можно усиливать или ослаблять свойства цвета. Для этой картины он использовал приглушённую палитру, смещённую к цветам, расположенным в одной части спектра.

Цитаты из книги: ЛИНИЯГеометрическая линия – это невидимый объект. Она – след перемещающейся точки, то есть ее произведение. Она возникла из движения – а именно вследствие уничтожения высшего, замкнутого в себе покоя точки. Здесь произошел скачок из статики в динамику.Таким образом, линия – величайшая противоположность живописного первоэлемента – точки. И она с предельной точностью может быть обозначена как вторичный элемент.ВОЗНИКНОВЕНИЕСилы, приходящие извне, преобразовавшие точку в линию, могут быть различными. Разнообразие линий зависит от числа этих сил и их комбинаций.В конце концов [происхождение] всех форм линий можно свести к двум случаям:1. приложение одной силы и2. приложение двух сил:а) одно- или многократное поочередное воздействие обеих сил,б) одновременное воздействие обеих сил.ПРЯМАЯЕсли одна приходящая извне сила перемещает точку в каком-либо направлении, то возникает первый тип линии, причем выбранное направление остается неизменным, и сама линия стремится двигаться по прямому пути бесконечно.Это – прямая, представляющая в своем напряжении самую сжатую форму бесконечной возможности движения....Среди прямых мы выделяем три типа, по отношению к которым все прочие прямые – лишь отклонения.1. Простейшая форма прямой – это горизонталь. В человеческом представлении она соответствует линии или поверхности, на которой человек стоит или передвигается. Итак, горизонталь – это холодная несущая основа, которая может быть продолжена на плоскости в различных направлениях. Холод и плоскостность – это основные звучания данной линии, она может быть определена как кратчайшая форма неограниченной холодной возможности движения.2. Полностью противоположна этой линии и внешне, и внутренне стоящая к ней под прямым углом вертикаль, в которой плоскостность заменяется высотой, то есть холод – теплом. Таким образом, вертикаль является кратчайшей формой неограниченной теплой возможности движения.3. Третий типичный вид прямой – это диагональ, которая схематичным образом под равным углом отклоняется от обеих вышеназванных и тем самым имеет к обеим равное тяготение, что и определяет ее внутреннее звучание, равномерное соединение холода и тепла. Итак: кратчайшая форма неограниченной тепло-холодной возможности движения...

geometry-and-art.ru

Работа № 10 Ломаные линии и сплайновые кривые

Цель работы: Изучение приемов работы с ломаными линиями и сплайновыми кривыми: кривая Безье, NURBS-кривая. Редактирование сплайновых кривых. Способы создания «скульптурных» поверхностей.

Введение

В этой работе мы более подробно познакомимся со способами моделирования сложных («скульптурных») поверхностей, которые впервые потребовались для создания форм новых автомобилей, самолетов, космических кораблей, многочисленных бытовых приборов.

	Первый автомобиль с паровой машиной – 1769 г.
	Автомобиль – 1896 г.
	Автомобиль фирмы Рено (Renault) – 2006 г.

В работе рассматриваются новые команды и термины, смысл которых мы будем раскрывать постепенно:

Материал для чтения

1. Команда Ломаная – .Позволяет построить ломаную линию, состоящую из отрезков прямых.

2. Сплайновые кривые. Термин «сплайн» происходит от английского слова spline. Так называется гибкая полоска стали, при помощи которой чертежники проводили через заданные точки плавные кривые. Раньше подобный способ построения плавных обводов различных тел, таких как, например, корпус корабля, кузов автомобиля был довольно широко распространен в практике машиностроения. Сплайном называли и разметочную веревку, кривизна которой регулировалась подвешенными грузиками (рис. 9.1). В результате форма тела задавалась при помощи набора очень точно изготовленных сечений – плазов. Появление компьютеров позволило перейти от этого механического метода к более эффективному математическому способу задания поверхности обтекаемого тела.

Рис. 9.1.

Два из наиболее общих типов сплайнов – кривые Безье и В-сплайны (би-сплайны). Типичным примером сплайнов являются также неоднородные рациональные NURBS-кривые («нурбс»-кривые).

3. Кривая Безье – . В начале 70-х годов профессор Пьер Безье, проектируя на компьютере корпуса автомобилей «Рено», впервые применил для этой цели уравнения, описывающие кривые, впоследствии названные его именем.

4. NURBS-кривая – . Сокращение (аббревиатура) NURBS обозначаетNon-UniformRationalB-Splines, то есть неравномерные рациональные B-сплайны. Это математические объекты для задания двумерных кривых и гладких поверхностей в трехмерном пространстве.

Рациональный (Rational) означает, что объект NURBS может быть описан с помощью математических формул.

Соотношение между сплайнами различных типов качественно иллюстрируется рис. 9.2.

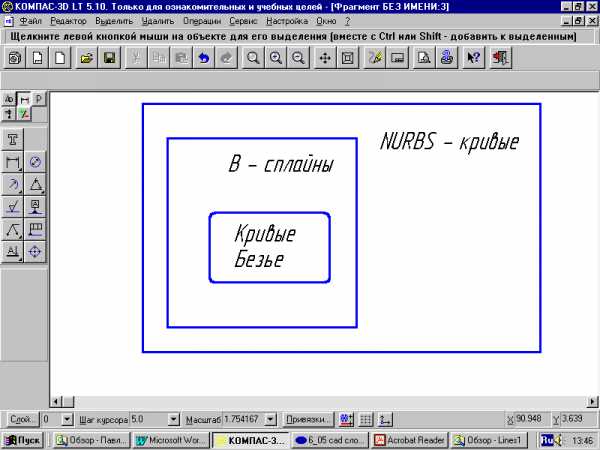
Рис. 9.2.

studfiles.net