Как решать задачи по математике, если не знаешь с чего начать. Задача любая по математике
Как можно решить задачу по математике
Многие из нас хотя бы раз сталкивались со сложной задачей по математике, решения которой, кажется, не существует вовсе. Специально для людей, которые не оставляют дела на полпути, мы разработали общую схему решения задач по математике, которая не только поможет вам прийти к правильному ответу, но и сбережет вашу нервную систему.
Какие бывают задачи по математике
Задачи по математике классифицируются по разным признакам. Например, по содержанию они бывают текстовые, вычислительные, задачи на доказательство или комбинированный тип.
По функциям можно выделить дидактические задачи, а также развивающие и контролирующие.
По роли в обучении задачи бывают на усвоение материала, на изучение математической символики, на получение математических навыков, а также общие задачи на развитие.
Спешим вас обрадовать: любую из вышеперечисленных задач можно решить при помощи правильного алгоритма, который предложен нами ниже.
Как можно решить задачу по математике
Чтобы самостоятельно прийти к правильному решению, воспользуйтесь нашим алгоритмом.
Во-первых, определите, задачу на какую тему вы решаете. Это задача на нахождение неизвестного, задача с дробями, задание на логику или же закрепление знаний о квадратных или кубических уравнениях? Вы должны четко понимать, чего именно от вас хотят, формулами из какой темы вы будете пользоваться.
Теперь сосредоточьтесь на условии задания. В математических задачах, как правило, не бывает лишней информации. Это значит, что условие содержит только сведения, которые обязательно нужно использовать.
Изучайте условие до тех пор, пока вы четко не осознаете, с чем имеете дело и не представите, сколько вам придется выполнить действий и на какие формулы ссылаться.
Теперь сформулируйте условие своими словами, чтобы вы руководствовались собственными мыслями и знаниями при решении. Лучше всего после изложения записать вашу формулировку в кратком виде, выписав важную информацию, чтобы не упустить ее из виду при решении. Просто в виде заметок выпишите основные сведения.
Теперь изобразите задачу в виде рисунка. Это не относится к задачам на логику, но другие математические задачи легче воспринимаются, когда перед глазами есть конкретные образы. Сравните готовый рисунок с условием задачи и исправьте помарки, если они есть. Рисунок может быть диаграммой или графиком. Можно просто изобразить несколько линий. Решать вам.
Попробуйте вспомнить, не решали ли вы подобные задания в прошлом. Скорее всего, хотя бы часть задачи уже была решена в подобном задании, вам просто нужно провести параллель с ним. Для этого попробуйте выбрать формулы, на которые вы полагаетесь при решении. Если ранее вы уже использовали эти формулы, поступите по такому же принципу.
Если вы все еще не видите ни одного решения, изучите похожие задачи с решением в интернете. Как правило, после этого процесса люди осознают, с чем столкнулись и продвигаются в решении.
Выбираем нужную информацию
Итак, вы уже определились, какими формулами пользоваться. Выпишите эти формулы, даже если вы их знаете наизусть. Информация, которую мы видим, лучше перерабатывается нашим мозгом.
Возможно, что для данного типа задач в учебнике уже предусмотрен определенный алгоритм. Если его нет, то запишите, как вы собираетесь решить задачу. Записывайте последовательно каждый свой шаг.
Если вы не можете сориентироваться в решении задания, найдите в учебнике или в интернете похожую задачу, но на уровень легче, и решите сперва ее.
Теперь проверьте, всю ли информацию, данную в условии, вы собираетесь использовать. Возможно, вы упустили из виду деталь, которая изменит ход решения или ответит на ваши вопросы.
Попробуйте представить, каким должен быть ответ. Любая задача не может иметь бесконечное количество ответов. Какие-нибудь ограничения (отрицательное число, определенный диапазон) должны присутствовать.
Рекомендации по ходу решения
Когда решаете задачу, не уходите от намеченного плана. Если вы зашли в тупик, то вернитесь в место, которое вызвало сомнения, и перепишите ваш план заново, начиная с этого места.
Когда вы пришли к ответу, сравните его с тем ответом, который вы предполагали ранее. Если результат значительно отличается от ожидаемого, возможно, где-то вы допустили ошибку.
Если вы не смогли получить ответ, попробуйте составить другой план решения. Наверняка тема, которую вы не понимаете, предоставляет множество формул, попробуйте использовать другие. Вполне вероятно, что вы просто не решились пойти по более сложному пути.
Типичные ошибки при решении задач
Чтобы лучше понять суть алгоритма, рассмотрим самые распространенные ошибки учащихся, которые заводят их в тупик и не дают получить верный ответ.
Во-первых, многие принимаются за решение, не зная общепринятых правил, определений или формул. Изучите материал по теме полностью, прежде чем приступать к решению.
Часто учащиеся знают правила и формулы, но попросту не понимают их. Вы должны не просто изучить материал, вы должны в него вникнуть и осознать цель применения полученной информации.
Бывает, что человек прекрасно владеет всем материалом и понимает его, но для конкретной задачи выбирает совсем не ту формулу. Попрактикуйтесь на более легких задачах, чтобы научиться выбирать правильные формулы для решения.
Одна из самых распространенных ошибок – это пренебрежение внимательным изучением условия задачи. Как говорят многие опытные педагоги, половина ответа уже дана в задании, и это абсолютная правда. Верное понимание условия дает правильное направление мыслей при решении.
Очень обидной, но распространенной проблемой многих учащихся, является постоянное допущение вычислительных ошибок. Профессиональные педагоги отмечают, что много талантливых учеников просто не обращают внимания на элементарные вычисления, вследствие чего и приходят к неправильному ответу.
Распространенная ошибка при решении геометрических задач – это пренебрежение свойствами геометрических фигур. Часто такие задачи основаны на этих свойствах, поэтому это первое, на что следует обратить внимание.
Когда учащиеся производят определенные действия по формулам, нужно помнить о свойствах математических операций. Так, скобки раскрываются в начале, после чего идет умножение с делением, а потом – сложение и вычитание. Этот материал преподается еще в начальной школе, но многие люди забывают о нем.
Полезные советы
Теперь, когда вы знаете, как решить задачу по математике, попытайтесь понять, что сильная усталость или нервное перенапряжение будут большой помехой правильному ходу решения. Дождитесь, когда вы будете отдохнувшим и сможете сконцентрироваться на задании полностью, а уже тогда приступайте к решению.
Кроме того, придумайте себе мотивацию для качественной работы. Именно она дает нам силы и заставляет выполнять задания, которые мы считали слишком сложными для себя.
nauchniestati.ru
Как научить детей решать задачи по математике: советы именитых педагогов и простых мам
Научить детей решать задачи по математике — дело учителя, но и родители не должны оставаться в стороне, если их чадо «тормозит» в этом вопросе. Одним учебником математики сыт не будешь. Ведь если научить ребенка самостоятельно решать задачи в 1-3 классах, дальше он будет щелкать как семечки не только задачи по математике, но и по физике, химии, геометрии и др. И самое главное — этот навык пригодится ребенку в жизни!
 vogazeta.ru
vogazeta.ru
В статье Как научить ребенка математике мы подробно писали, из каких 4 частей состоит любая задача и что нужно сделать в первую очередь, чтобы ребенок понял, чего от него хотят и как ответить на вопрос задачи. Уяснив алгоритм решения задач, ребенок сможет самостоятельно решить практически любую задачу, даже несмотря на то, что они все кажутся такими разными.
Основные типы задач по математике: краткий конспект
Небольшой ликбез, т.к. далеко не все родители учились в педагогических ВУЗах и владеют методикой преподавания. Пробежимся по теории, чтобы понимать, кто, кому и чего «должен». Зная ключевые моменты, вам будет проще помочь ребенку в решении задач, которые вызывают у него сложности, вы сможете определить, где пробелы в знаниях и что нужно «подтянуть» в каждом конкретном случае.
 iqsha.ru
iqsha.ru
Рассмотрим самые распространенные виды задач в начальных классах.
1. Простые задачи на сложение и вычитание
К этой группе относятся несколько задач, но для всех есть общие рекомендации:
- Решаются в одно действие.
- Иногда удобно составить уравнение.
- На их примере ребенок должен научится выполнять краткую запись.
- Если краткого условия недостаточно, нарисовать рисунок. Если не помог рисунок, показываем на конкретных предметах и производим действия с ними.
- Четко усвоить, что «+» — это прибавить, увеличить, а «-» — уменьшить, отнять, вычесть.
- Хорошо запомнить компоненты арифметических действий:
слагаемое + слагаемое = суммауменьшаемое — вычитаемое = разность
- Понять разницу между словами «стало» и «осталось». Четко понимать, что значит «на … меньше», «на … больше».
- Важно понять и запомнить: чтобы узнать, НА СКОЛЬКО одно число больше или меньше другого, нужно из большего числа вычесть меньшее.
- Важно понять и запомнить: чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
- Важно понять и запомнить: чтобы найти неизвестное уменьшаемое, нужно к вычитаемому прибавить разность.
- Важно понять и запомнить: чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
Задачи с косвенным вопросом
Это самые коварные задачи из этой группы. Внимательно прочитайте условие — и поймете почему.
На стоянке у первого подъезда 7 машин. Это на 2 машины больше, чем на стоянке у второго подъезда. сколько машин на стоянке у второго подъезда.
2. Составные задачи на сложение и вычитание
Эти задачи решаются двумя и более действиями.
Есть несколько способов решения:
- по действиям с пояснениями;
- по действиям с вопросами;
- выражением.
В решении таких задач главное:
- найти главное и сделать краткую запись;
- разложить эту задачу на несколько простых и составить план решения;
- помнить главное: по двум данным находим третье.
3. Задачи на понимание смысла действий умножения и деления
- Важно запомнить названия компонентов действий и понять их смысл:
1-й множитель х 2-й множитель = произведениеделимое : делитель =частное
- Ребенок должен понимать, что 1-й множитель показывает, КАКОЕ число повторяется а 2-й множитель показывает — СКОЛЬКО РАЗ оно повторяется.
Это очень важно для правильной записи в задачах, иначе получится бессмыслица.
Советы о том, как научить ребенка осознанно относиться к умножению и делению, вы найдете в нашей статье Как научить детей быстро считать: математика до школы. Если возникли проблемы с решением задач на умножение — сдайте чуть-чуть назад, закрепите осознание этого арифметического действия.
4. Простые задачи на умножение и деление
- Очень важно понять и запомнить разницу «в «, «на».
«Во сколько раз» или «на сколько»? Предлог «на» — это сложение или вычитание, а «в» — умножение или деление.
- Важно понять и запомнить: чтобы узнать, во сколько раз одно число больше или меньше другого, нужно большее число разделить на меньшее.
5. Составные задачи на все 4 арифметические действия
6. Задачи на цену, количество, стоимость
7. Задачи на движение
Это отдельная обширная тема, вернемся к ней позже.
Типичные ошибки в решении задач
Ошибка №1. Ребенок невнимательно прочитал условие задачи.
Часто бывает так, что ошибки возникают от невнимательности. Так часто бывает в задачах с косвенным вопросом. Ребенок смотрит на цифры, вроде все логично, но… не верно.
Например: «У Маши 8 конфет, это на 2 меньше, чем у Кати. Сколько конфет у Кати».
Ребенок видит «на 2 меньше» и делает «логичный» вывод, что надо отнять. Отнять можно от бОльшего числа, т.е. сразу напрашивается решение 8-2=6. И ответ: 6 конфет у Кати. А ответ-то не тот! Если внимательно почитать условие, то станет понятно, что у Кати конфет больше чем у Маши. И вовсе тут не отнимать надо.
Как исправить ошибку. Сразу разберитесь с условием, поможет краткая запись.
Ошибка №2. Ребенок допустил ошибку в решении.
Когда в задаче несколько неизвестных, решение затрудняется, требуется выполнить не одно действие, а придумать целую цепочку рассуждений.
Как исправить ошибку. Для начала определим, каких данных нам не хватает. Решаем по действиям. Находим нужные числа (помним правило: по двум неизвестным находим третье), подставляем их и отвечаем на вопрос задачи.
Ошибка №3. Неправильная запись ответа.
Часто ребенок пишет не то пояснение.
Как исправить ошибку. Нужно внимательно прочитать вопрос задачи. Уяснить раз и навсегда, что ответ начинается с числа, а дальше пишем, что требовалось найти (переписываем формулировку вопроса задачи).
Творческий подход в решении задач
 www.craftykidsathome.com
www.craftykidsathome.com
- Учите ребенка рассуждать.
- Придумывайте задачи с лишними или недостающими данными.
Пусть ребенок сам вычеркнет лишнее, те данные, которые не влияют на решение.
- Дайте условие, а ребенок пусть сам придумает ответ.
- Пусть ребенок сам составит обратную задачу.
- Придумать несколько задач на одно решение.
- Придумать, как решить задачу другим способом и объяснить его.
На школу надейся, а сам не плошай
Заглянем в педагогику и «расшифруем» мысли умных и заслуженных, исходя из сегодняшних реалий.
В далеком 1867 году К. Ушинский сказал: «У хороших преподавателей дело выходит так, что арифметическая задача есть вместе занимательный рассказ, урок сельского хозяйства или домашней экономии, или историческая или статистическая тема и упражнение в языке».
«Расшифровка» следующая.
- Ученика нужно поставить в такие условия, чтобы он оказался в эпицентре событий, т.е., решая задачу, видел ее применение в жизни.
Не всегда задачи в школьном учебнике «вдохновляют» современных школьников. Многим не ясно условие по одной простой причине: ребенок не имеет представления о том, что говорится. Например, задача про надои и бидоны с молоком, а городской «деть» и корову-то в глаза не видел, не то, что тонны молока в бидонах. Или в задаче использованы такие значения, которые в жизни нереальны — это затрудняет восприятие, т.к. ребенок все воспринимает буквально.
Задача родителей — помочь ребенку ПОНЯТЬ условие. Любым способом: хоть рисуй, хоть танцуй.
- К решению задач нужно подходить творчески.
Интерес заставляет ребенка быть активным, а активность в свою очередь усиливает внимание.
В каждодневной жизни нам то и дело приходится решать задачи. Привлекайте ребенка, задавайте вопросы, просите совета. Например, тема ремонта. Вычислить метраж комнаты; просчитать нужное количество краски, зная расход на метр квадратный; купить линолеум, зная длину и ширину комнаты; просчитать, какой метраж выгоднее, если есть напольное покрытие шириной 2, 5 метра и 3 метра, чтобы меньше остатков было и по цене вышло выгоднее. Купить ткань на пошив постельного белья, зная размеры матраса. Примеров масса! И это работает гораздо эффективнее, чем «бездушная» задача в учебнике, которая совершенно не привязана к жизни и не вызывает эмоциональный отклик.
- При решении жизненных задач у ребенка помимо всего прочего развивается наблюдательность, речь, появляется рабочее настроение, развиваются творческие способности и самостоятельность.
Через некоторое время вы заметите, что ребенок различными способами комбинирует информацию, с легкостью составляет задачи сам, находя идеи в окружающем мире, а не высасывая из пальца.
- Когда ребенка просят составить собственную задачу, нужно следить и за содержанием, и за решением. Задача должна быть осмысленной и целесообразной.
Например, нельзя допускать таких «ляпов», как «Я съел 13 желтых груш и 20 зеленых яблок. Сколько фруктов я съел?» Задача теряет смысл, если она оторвана от жизни.
- От задачи надо идти к примеру, а не наоборот.
Дети мыслят не абстрактно, а конкретными образами. Пример 12-6 ни о чем не говорит, а вот ситуация, когда из 12 человек 6 уже купили билеты на футбольный матч — это совсем другое дело. Тут ребенок не задумываясь ответит, что оставшиеся шестеро очень рискуют, нужно поторопиться, иначе билетов может не хватить и придется сидеть у телевизора, вместо того, чтобы активно скандировать на трибунах в поддержку любимой команды.
Лебединцев в своей книге «Введение в современную методику математики» писал: «То влияние, которое может оказывать обучение счислению и вообще математике на умственное развитие детей, находится в прямой зависимости от материала, которым мы пользуемся при обучении; если в учебном материале будут преобладать отвлеченные упражнения в действиях и хитроумные задачи с условиями, лишенными внутренней связи и, по существу, далекими от жизни, то, упражняя учащихся на таком материале, мы, может быть, и выработаем у них формальные навыки в вычислениях и, пожалуй, изощрим их ум для разгадывания разных ребусов и головоломок, но отнюдь не сделаем их более способными к правильному мышлению в жизни или какой-либо области знания…».
Французский педагог Жан Мосе тоже был уверен, что «заставлять ребенка начинать с отвлеченного правила и затем предлагать ему задачи — это значит идти наперекор ходу развития человеческого ума…».
Практические советы по решению задач от реальных мам
 fb.ru
fb.ru
Что нам Ушинский, Лебединцев и Мосе, спросим у тех, кто «из нашей песочницы». Как они помогают своим детям решать задачи по математике, что «работает», какие приемы на практике доказали свою эффективность и помогли повысить успеваемость.
Татьяна, мама учеников 4 кл. и 6 кл.
«Я знаю, что особую сложность у детей вызывают задачи на скорость, поэтому начала готовить своих мальчишек к этому уже с 1 класса. Когда ехали к бабушке в Пинск, говорили о скорости, засекали время, считали сколько мы проехали км, смотрели на знаки и вычисляли сколько нам останется времени, если мы будем ехать с такой же скоростью и сколько, если папа будет ехать с другой. В общем, я очень удивлялась, когда мои пацаны на скорость задачи решали как орехи. Я поняла, что в моем детстве не хватало практического представления того, о чем говорилось в задачах».
Ольга, мама ученика 1 кл. и ученицы 4 кл.
«С задачами старшая плохо дружит)) Почти всегда приходит за помощью. Стараюсь выработать алгоритм решения, но частенько упираюсь в «лень подумать». Если совсем «затык», рисуем схемы. На дополнительные задачи совсем нет времени, а сама по своей воле заниматься ими дочь точно не будет)) Иногда встречаются задачи с некорректно поставленным вопросом, тут приходится помогать с формулировкой ответа.
Младшего усадить за математику очень сложно. В те редкие моменты, когда дело доходит до задач, он их решает в уме и выдает ответ устно).»
Вероника, мама учеников 2 кл. и 4 кл.
«Младший задачи решает без проблем, но ненавидит чертить схемы к ним и писать пояснения. Старший ходит на факультатив по математике, дома домашку сам делает».
Катерина, мама ученика 2 кл. и ученицы 5 кл.
«Сын отлично справляется сам. Он такие схемы рисует, что я иногда в шоке)). Если за помощью обращается дочь, стараюсь упростить условие задачи до понятных образов, а потом она сама догадывается, как сложную модель решить».
Татьяна, мама ученицы 5 кл.
«Чаще всего прибегаем к рисованию. Прямо вот как по условию… садимся и рисуем, как есть. Так сказать, наглядность помогает. Велосипедист выехал… значит рисуем человечка на велосипеде, город из которого он выехал и тд)))) Если катер плывет по течению, рисуем море, волны)))))) С пояснениями никогда исправлений со стороны учителя не было, да и у нас, собственно, тоже вопросов не возникало. Смотри по условию, что спрашивают — и пиши ответы возле каждого действия».
Наталья, мама ученика 5 кл.
«Приходилось объяснять дроби на примере сломанных карандашей, порванных в клочья бумажек. В гостях в тот момент был друг-проектировщик, он именно так решил наглядно пояснить сыну задачу. Я обычно прибегаю к помощи рисования. В задачах на скорость/время/расстояние рисовали целые истории: кто куда и на чем поехал, кого встретил по дороге и в какой момент. Порой решение задач превращалось в мультфильм, одного черновика обычно мало. Несколько раз решали задачи всей семьей: мама отдельно от папы, потом сравнивали результаты и каждый объяснял ребенку свой «самый рациональный и простой» способ. Как правило, у мужчин своя логика)), мое решение обычно отличается от папиного».
Уважаемые читатели! Делитесь в комментариях своими находками и сложностями в решении задач по математике с детьми. будем разы разобраться вместе и помочь советами и полезными статьями на интересующие вас темы.
rastishka.by
Как решать задачи по математике?
Как научить ребенка решать задачи по математике?
Решая задачу о блинчиках мы увидим, что:
• сложными могут оказаться и простые с виду задачи.
• Учить ребенка думать можно и нужно на примере простых задач. Если же с первых классов школы задурить ему мозги, то думать он не научится никогда. Но обнаружится это в классе 6-7. Слишком поздно.
Статья будет длинная и нудная. Она
может быть интересна исключительно родителям, желающим научить собственного ребенка понимать математику. Научить думать.
Простоe и сложное
Чем проще принцип, тем сложнее его доказательство и длиннее объяснение собственные наблюденияК примеру, большая теорема Ферма.
Хn + Yn = Zn
Теорема простая, понять ее способен даже ученик начальной школы. А вот доказать её удалось лишь спустя три столетия, в 1994 г. Говорят и сейчас не более двухсот математиков в мире понимают это доказательство. Я в их число не вхожу
Как(не)научить понимать: "Принцип короткого замыкания"
Главный принцип (не)успешного обучения, который я обнаружил - "принцип короткого замыкания":Понимание не возникает из простоты, оно возникает из сложности. Простота и понимание возникают в процессе и являются результатом обучения . И категорически запрещено укорачивать этот путь!
Именно на этом пункте и спотыкается традиционная школа.
«Игровой подход», как ласково они это называют, цветные картинки, два притопа – три прихлопа … Это НЕ обучение, а его имитация. (Я уже писал о «самолетопоклонниках» Ричарда Фейнмана в книге «Школа понимания».)
«Ах, как все просто и понятно!»
«Ах, как понятно объясняет учительница! Дети все схватывают с первого раза!» Только вот беда: со второго раза, когда встречается чуть видоизмененная задача, путаются и заявляют, что «Они этого не проходили!». Что является абсолютной правдой. И «заслуженному учителю» вновь приходится «в игровой форме» исполнять танец с бубном около «интерактивной доски».
Но и танцевать большинство школьных учителей мастера не великие. Им бы лучше в хор: орать на детей они умеют громко, эмоционально, с душой …
Да, ирония злая. Но большинством школьных функционеров, маскирующихся под Учителей, вполне заслуженная.
На выходе «игрового подхода» к 9-11 классам мы имеем ужасающую статистику непонимания математики, равно, как и других предметов.
Если уже известный ответ задачи, готовое "решение" препарировать, разложить на составляющие, «понятно объяснить», то, естественно, ребенок запомнит «решения» десятка задач. И, также естественно, не научится их решать.
Объяснить готовый ответ и решить задачу – две гигантские разницы!
«Главное — возбудить аппетит и чувства: иначе воспитаете осла, нагруженного книгами …» МонтеньКто должен учить?
Основам науки должен учить тот, кто сам эти основы понимает.
Научить думать сможет только тот, кто умеет думать сам.
В начальной же школе работают … ну, вы сами это знаете.
Почему-то считается, что основам математики может научить кто угодно, даже педагог, который сам не умеет решать простейших задач. Но почему-то потом, в старших классах дети массово отказываются понимать математику и что-либо вообще.
Итак,
Задача о блинчиках
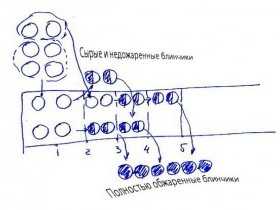
«Мама жарит блинчики с творогом. Каждый блинчик она обжаривает с двух сторон: 2 минуты с одной и 1 минуту с другой. На сковороду одновременно умещаются 4 блинчика. Вопрос: за какое минимальное время мама обжарит 7 блинчиков?»
…Поместите эту задачу в раздел самых сложных задач профильного ЕГЭ и процентов 80 выпускников с ней не справятся и/или потеряют неоправданно много времени. Ожидание «подвоха» не позволит выпускникам, чьё математическое мышление за 11 лет так и не было развито, найти верное решение. Смутное чувство интуиции заставит их сомневаться, перебирать варианты в поисках «красивого» ответа...
Решение задачи
Задачи в начальной школе простые, даже примитивные. Ответ получается методом перебора плюс немного здравого смысла и чуть-чуть воображения…
…Сначала мама обжаривает 4 блинчика за 3 минуты ( 2+1=3).
Затем оставшиеся 3 блинчика (7 - 4 = 3), тоже за 3 минуты.
Итого 6 минут. Вроде все верно?
Но:
• Как доказать, что решение верное? Не может же ответ быть настолько простым! Прямо как теорема Ферма ...
• И как решить эту же задачу, если мама – директор «блинной фабрики» и за день обжаривает N блинчиков?
Оставим в покое маму – фабриканта и вернемся к условию.
Анализ решения задачи
Сразу бросается в глаза неэффективность использования сковороды. Как-то некрасиво, не по-школьному получается. Незрелый ум школьника замечает: КПД сковороды слишком низкий, одно место при второй обжарке пустует. Сковорода греет воздух, а масло горит …. Можно ли как-нибудь использовать одно свободное место во втором цикле обжарки?
Разумный вопрос: его следует задать и поискать ответ.
Метод перебора
Перебор вариантов это метод. Но не столько метод решения, сколько метод оценки данных, используя который иногда можно нащупать решение.
Но нащупать - не значит доказать, что оно верное.И сомневающийся школьник продолжает в поисках правильного ответа перебирать варианты … То есть действует методически неверно.
«Предположим, что …» - метод
Предположим, что для обжарки требовалось бы три «неделимых» минуты - блинчики обжаривались бы за один раз с одной стороны. Решение оказалось бы настолько тривиальным, что и решать тогда было бы нечего!
Но в условии сказано: блины переворачивают!
Поэтому количество вариантов возрастает и школьник судорожно ищет «что в какую формулу вставить, и что на что разделить» (по ироничному наблюдению за отличниками академика В.И.Арнольда, одного из крупнейших математиков ХХ века). Смутное чувство интуиции шепчет: здесь что-то не так, не все так просто. Человек бессистемно перебирает варианты, пока не доходит до «перестановок из N по M». Но и комбинаторика в младшешкольной задаче выигрыша во времени не дает ...
Человеку кажется: он что-то упустил и судорожные эксперименты с перекладыванием блинов, попытки вспомнить «похожие» задачи и «волшебные» формулы продолжаются. Пока уставший от непродуктивной механической деятельности ум не ошибется и не «нащупает красивый ответ»: 5 минут.
Именно такое «решение» получила учительница начальных классов в школе, которую посещал мой сын. Он тогда поспорил с учительницей, но она настаивала: «Все-таки здесь получается скомбинировать! Сейчас не помню как именно, но точно – получается!». Задачу она дала на уроке «Умники и умницы», поэтому нашлась еще пара «Умников», поддержавших «красивое» решение.
Это вообще не шутка.
«Ум человеческий склонен верить непонятному» ТацитМатематическая логика и интуиция
Неразвитое мышление активизирует «интуицию». Но ум человеческий не приспособлен адекватно воспринимать мир цифр. Это, кстати, научно подтвержденный факт.
Например: как вы думаете, сколькими способами можно разложить колоду всего лишь из 52 карт? Правильный ответ шокирует: неужели мы способны НАСТОЛЬКО ошибаться?!
Чтобы шок состоялся, прикиньте ответ, а потом посчитайте на калькуляторе факториал 52. Пожалуй, это больше, чем количество атомов в известной Вселенной ...
… Без специальной подготовки ум человеческий воспринимает мир цифровой СЛИШКОМ уж несовершенно. Поэтому и возникает «смутное чувство интуиции».
Решение задачи о 6 блинчиках
Предположим, что теперь мама обжаривает только 6 блинчиков. Можно ли теперь уложиться в 5 минут?
Решение.
Итого: 2 + 1 +1 + 1 = 5 минут.
Минуту удалось-таки сэкономить!
Хотя и тут разбазаривание ресурсов налицо: последнюю минуту на сковороде было только 2 блина … . Как говорится, абсолюты в реальном мире недостижимы, считай – не считай …
Арифметика или геометрия? Визуализация VS абстрагирования
Сложно было следить за текстовым изложением решения, не правда ли? А теперь представьте, каково это детям!..Не проще ли изобразить процесс решения графически? Попросту – нарисовать?!
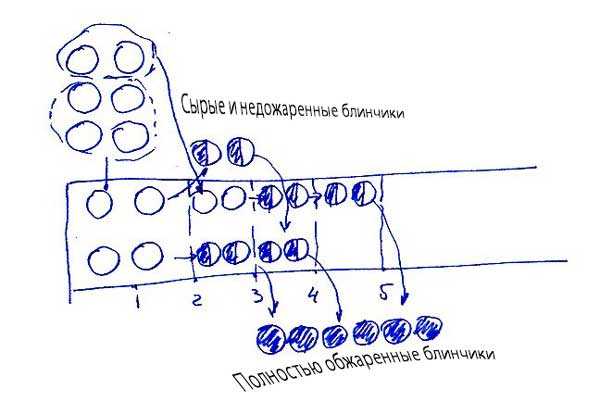
... Детям исключительно полезно решать задачи подобным образом.
С помощью рисунков они приучаются думать (а не запоминать типовые «решения»). Оперирование образами формирует связное, логическое мышление, они узнают, что такое понимание.
Но вряд ли хотя бы 0,1% учителей математики представляет, как работает ум и что в нем происходит во время решения математической задачи! В МПГУ этому не учат.
Родителю – на заметку: всемирно известный академик В.И Арнольд славился доходчивым стилем преподавания и геометрическим подходом к традиционным разделам математики. А также жесткой критикой попыток американцев и, особенно, французов излагать математику на излишне высоком уровне абстракции. "Это великий-то математик?,- удивитесь вы,- "Представитель самой абстрактной из всех наук?!"
Вот именно.
Доказательство очевидного: «правильный ответ» задачи
Как узнать, верен ли полученный ответ? Проверка решения это составная часть решения, не менее важная, чем само решение.
Как доказать, что за 5 минут 7 блинчиков обжарить нельзя, а 6 - можно?..
Дроби появляются незаметно …
Как максимальная скорость автомобиля: не обязательно «выживмать» все, можно двигаться и медленнее. Но быстрее - невозможно.
Хотя для такой оценки и требуется понимание дробей, но не очень глубокое.
Дроби, кстати - раздел арифметики, в котором массово «плавает» большинство школьников на ЕГЭ (???). Поэтому, насколько это задача для 3 класса … зависит от способа ее подачи и квалификации «подающего» блинчики к столу решающих задачу
Итак:
при полной загрузке сковороды для обжарки 7 блинчиков требуется больше 5 минут. Не надо больше мучиться и «комбинировать».
А вот для 6 блинчиков можно варианты и поискать.
Задача о блинной фабрике
А что насчет мамы – блинного капиталиста? Если ребенок уяснил метод решения, то теперь ему не составит труда масштабировать решение на любые количества. Но скажите: разве это было очевидно до того, как мы прошли весь этот довольно сложный путь?!
Единственный способ научить ребенка решать задачи это научиться решать их самому. Не так уж и сложно взрослому и заинтересованному человеку научиться решать задачи младшей школы, не так ли? Было бы желание. А если желание отсутствует у наиболее заинтересованных в ребенке людей ... тогда дело швах. Сегодня рассчитывать на школу, также, как на репетиторов - абсолютно дохлое дело.
Вернитесь к началу статьи и представьте, что все это происходило в классе. Получилось? А потом представьте, то же самое в присутствии репетитора и ответьте себе на два вопроса:
«Соображайте, мужчина!», - как четверть века назад строго заметила мне смотрительница около турникета метро на «Комсомольской», когда я по ошибке сунулся не в те ворота.
butorov.ru
Сказочные задачи по математике. |
Сказочные задачи по математике – это задачи со сказочным сюжетом и (или) задачи со сказочными героями.
Занимательные задачи сказочного характера занимают видное место в процессе обучения математике. Казалось бы, сказка и математика – понятия несовместимые. Поэтический образ и абстрактная мысль, сухое рассуждение! Однако сказочная форма позволяет ввести необычные, увлекательные ситуации в математические задачи со сказочным сюжетом. Тем самым эти задачи оживляются. Именно такое соединение благоприятно для обучения, поскольку через сказочные элементы учитель может найти путь в сферу эмоций ребенка.
Действительно, опыт проведения олимпиад, недель математики, работа кружков, математические вечера или часы занимательной математики подтверждают, что встреча школьников со знакомыми героями сказок не оставляют их равнодушными. Желание помочь попавшему в беду герою, разобраться в сказочной ситуации – все это стимулирует умственную деятельность ребенка, развивает его интерес к математике.
В то же время важна и обратная связь: встреча в задачах со сказочными героями в мире математики побуждает ребенка еще раз прочитать литературное произведение, поразмыслить над ним. При составлении задач в сказочной форме надо стремиться, чтобы ситуации задач соответствовали духу самой сказки: борьба за справедливость Ивана и коварство Кощея Бессмертного, верность дружбе неунывающего Буратино и стремление поживиться за чужой счет неразборчивых в средствах лисы Алисы и кота Базилио, стремящийся к цели Муравьишка и т.д.
Симпатии детей на стороне положительных героев. Добро торжествует. Зло наказывается, отрицательные качества высмеиваются. Сказки и через задачи продолжают воспитывать школьников.
Приведем примеры таких задач.
Задачи со сказочными героями.
Задача 1.
Красная Шапочка несла бабушке 14 пирожков: с мясом, с грибами и с капустой. Пирожков с капустой – наибольшее количество. Причем, их вдвое больше, чем пирожков с мясом. Сколько пирожков с грибами?
Решение:
Пусть пирожков с мясом 2, тогда с капустой 2*2 = 4 (пирожка). Следовательно, с грибами 14 – (2+4) = 8 (пирожков). Но в этом случае пирожков с капустой не наибольшее количество.
Пусть пирожков с мясом 3, тогда с капустой 3*2 = 6 (пирожков). Следовательно, с грибами 14 – (3+6) = 5 (пирожков). Этот результат соответствует условию задачи.
Ответ: 5 пирожков с грибами.
Задача 2.
Лиса Алиса и кот Базилио привели Буратино на пустырь. – Это поле чудес: если закопаешь золотые монеты, то наутро вырастет дерево, на котором в 3 раза больше золотых монет. Затем полученные монеты можно снова закопать в землю и снова вырастет дерево с монетами. Так можно снять несколько урожаев. Мы можем посторожить ночью эти монеты.
В награду за услуги лиса и кот потребовали отдавать после каждого урожая 9 монет. Подумав немного, Буратино не согласился с их требованием. Он заявил, что после двух урожаев у него совсем не останется денег. Уж лучше он сам посторожит.
Сколько золотых монет было у Буратино?
Решение:
Второй урожай даст 9 монет. Значит, во второй раз Буратино посадит 9:3=3 (монеты). Первый урожай даст 3+9 = 12 (монет). Следовательно, в первый раз Буратино посадит 12:3 = 4 (монеты).
Ответ: 4 монеты.
Задача 3.
Возраст старика Хоттабыча записывается числом с различными цифрами. Об этом числе известно следующее:
- если первую и последнюю цифры зачеркнуть, то получится двузначное число, которое при сумме цифр, равной 12, является наибольшим;
- первая цифра больше последней в 4 раза.
Сколько лет старику Хоттабычу?
Решение:
Наибольшим двузначным числом с суммой цифр, равной 13, является 94.
Пусть последняя цифра 1, тогда первая цифра 1*4 = 4. Но такая цифра в числе уже есть – ведь цифры различные.
Пусть последняя цифра 2, тогда первая цифра 2*4 = 8. В этом случае все цифры различные.
Ответ: 8942 года.
Задача 4.
Два медвежонка нашли головку сыра. Они долго спорили, как ее поделить, но никто не хотел уступать. Мимо пробегала лиса. Узнав, о чем сор, она предложила помочь.
Разломив головку сыра на две части так, чтобы одна из них была полкилограмма, а другая меньше, она спросила, усмехаясь: – Куски равны?
Жадные медвежата дали отрицательный ответ. Тогда лиса откусила от большей части, но так, чтобы от нее остался кусок меньше, чем другая часть, и повторила вопрос. И на этот раз медвежата сообщили, что получились неравные части. После этого лиса повторила откусывание еще 9 раз, каждый раз откусывая одинаковое количество сыра. В результате остались маленькие кусочки один из них оказался на 20 г больше другого.
Лиса заявила, что медвежатам трудно угодить. Она отправила оба кусочка в рот и, вильнув хвостом, скрылась в кустах.
Какова была масса головки сыра?
Решение:
Лиса всего откусила 10 раз – от каждой части поочередно по 5 раз. Значит, от каждой части откушено одинаковое количество сыра, т. е. вторая часть содержит сыра на 20 г меньше, чем первая. Первоначальная масса головки сыра была 500+(500 – 20) = 980 (г).
Ответ: 980 г.
Задача 5.
Поросята Ниф-Ниф и Нуф-Нуф бежали от волка к домику Наф-Нафа. Волку бежать до поросят ( если бы они стояли на месте) 4 мин. Поросятам бежать до домика 6 мин. Волк бежит вдвое быстрее поросят. Успеют ли поросята добежать до домика Наф-Нафа?
Решение:
Волку бежать до домика Наф-Нафа 4+6:2 = 8(мин.).
6<7, значит, поросята успевают добежать до домика Наф-Нафа.
Ответ: успеют.
Задача 6.
Буратино, Мальвина и Пьеро, спасаясь от Карабаса Барабаса, выбежали на берег озера. Мальвина и Пьеро сели на черепаху Тортилу. Буратино же места не хватило, поэтому он бросился вплавь. Буратино может переплыть озеро за 30 мин., а Тортила – в 3 раза быстрее (с грузом или без него). Карабас Барабас побежал вокруг озера, и на это ему потребуется 30 мин.
Как быстрее переплыть озеро всем беглецам?
На противоположном берегу Мальвина и Пьеро дожидались Буратино: они не знали, куда бежать.
Успеют ли Буратино и его друзья убежать от Карабаса Барабаса; Папа Карло находится в 18 мин. бега от Буратино и его друзей. Карабас Барабас бежит в 2 раза быстрее, чем Буратино и его друзья.
Решение:
Когда Буратино доплывет до середины озера, то Тортила успеет там встретить Буратино – ведь черепаха плывет в 3 раза быстрее, чем Буратино. На середине озера Буратино будет через 30:2 = 15 (мин). Следовательно, Тортила с Буратино достигнут берега через 15 + 15:3 = 20 (мин).
Через 30-20=10 минут после этого на место высадки беглецов подбежит Карабас Барабас. В это время беглецы будут от папы Карло в 18-10=8 минут бега. Карабасу Барабасу бежать до папы Карло 18:2=9 (мин). 8<9, т.е. Буратино и его друзья успеют убежать от Карабаса Барабаса.
Ответ: успеют.
Вторая часть этой задачи по математическому содержанию сходна с предыдущей задачей. Поэтому полезно разобрать эти задачи вместе, рассматривая предыдущую задачу как подготовительную.
Задача 7.
Муравьишка ходил в гости в соседний муравейник. Туда он шел пешком, а обратно ехал. Первую половину пути он ехал на Гусенице – ехал в 2 раза медленнее, чем шел пешком. А вторую половину пути он ехал на Кузнечике, ехал в 5 раз быстрее, чем шел пешком. На какой путь Муравьишка затратил времени меньше: в гости или обратно?
Решение:
На половину пути верхом на Гусенице Муравьишка затратил столько же времени, сколько на весь путь пешком. Скорость Муравьишки пешком в 2 раза больше, чем скорость его на Гусенице. Значит, Муравьишка затратил времени на путь в гости меньше, чем обратно.
Ответ: Муравьишка затратил времени меньше на путь в гости.
Задача 8.
Маленький Мук и королевский скороход соревновались в беге по дорожке длиной – 30 км, которая шла вокруг леса. По условиям соревнования выигрывает тот, кто обгонит другого, пробежав на круг больше. Скороход делает круг за 10 мин, а Маленький Мук за 6 мин. Оба бегут равномерно. Через сколько минут Маленький Мук обгонит скорохода?
Решение:
За каждую минуту Маленький Мук пробегает 30:6=5 (км), а скороход 30:10=3 (км). Когда соревнующиеся начали двигаться от старта А, то Маленький Мук начал удаляться от скорохода.
Если принять, что Маленький Мук должен пробежать на круг больше, чем скороход, то можно считать, что первый будет догонять второго. За одну минуту они сближаются на 5-3=3 (км). Но Маленький Мук будет догонять скорохода на расстоянии 30 км. Следовательно, Маленький Мук обгонит скорохода через 30:2=15 (мин).
Ответ: 15 минут.
Уважаемые коллеги!
Понравились ли Вам математические задачи со сказочными героями?
Какие еще Вы можете предложить сказочные задачи по математике?
repetitor-problem.net
интересные математические задачи и задания
Польза занятий логикой и математикой
Элементарные математические представления помогают сформировать в детском саду. Базовые математические способности развивают в школе.
А чтобы ребёнок научился рассуждать логически, мыслить нестандартно — обычных арифметических и геометрических задач недостаточно.
Уже в дошкольном возрасте желательно выработать привычку ежедневно выполнять задания и упражнения на развитие логического мышления.
Благодаря регулярным тренировкам:
- ребёнок учится рассуждать, анализировать и делать правильные выводы;
- развивает сообразительность, память, внимание и интеллект;
- успехи повышают самооценку, интерес к обучению в школе, вдохновляют на победы в математических олимпиадах и конкурсах.
Математические задачи по возрасту
Заинтересовать дошкольников 5-7 лет, учащихся начальных классов проще всего. Главное — предложить разнообразные занимательные задания, сделать процесс решения задач увлекательным, с элементами игры, и обеспечить умеренную сложность задач.
К 3-4 классу мотивация у школьника часто снижается. Родителям важно не упустить этот момент и объяснить ребёнку, зачем вообще заниматься математикой и учиться решать задачи.
Примеры заданий по возрасту
Занимательные задачи по типу
В плане регулярных тренировок в любом возрасте должно быть выполнение заданий минимум 5-7 типов. Это поможет комплексному развитию логики у ребенка, познавательных, творческих и математических способностей.
Среди самых интересных и популярных категорий заданий на логику и смекалку:
- Классические логические задачи. Учат детей анализировать текст, выделять главное, рассуждать и делать выводы.
- Арифметические ребусы. Отличная отработка ключевых мыслительных операций: абстрагирование, анализ и синтез, сравнение и другие.
- Задачи на закономерности, последовательности. Помогают развить аналитические способности и творческое мышление.
Примеры заданий по типу
logiclike.com
|
vsemzagadki.narod.ru
Как решать задачи правильно и с чего начать решение задачи
В этой статье Вы узнаете как решать задачи по математике, если не знаете с чего начать.
 Часто при решении задач школьники "входят в ступор" - в голове туман, мысли куда-то разбежались, и кажется, что собрать их уже не возможно.
Часто при решении задач школьники "входят в ступор" - в голове туман, мысли куда-то разбежались, и кажется, что собрать их уже не возможно.
Я хочу на примере решения задачи из Открытого банка заданий показать, какие простые действия нужно сделать, чтобы собраться с мыслями и как решать задачи правильно.
Как решать задачи. Задание B13 (№ 26582)
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 98 км. На следующий день он отправился обратно со скоростью на 7 км/ч больше прежней. По дороге он сделал остановку на 7 часов. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.
1. Внимательно читаем задачу. Возможно, несколько раз.
2. Определяем, о каком процессе идет речь в задаче, и какие формулы описывают этот процесс. Выписываем эти формулы. В данном случае это задача на движение, и формула, которая описывает этот процесс S=vt.
3. Выписываем размерность каждой переменной, которая входит в состав уравнения:
- S - расстояние - км
- v - скорость - км/ч
- t - время - ч
Знание размерности поможет нам при проверке получившихся формул.
4. Выписываем все числа, которые встречаются в условии задачи, пишем, что они обозначают и их размерность:
98 км - расстояние между городами,
7 км/ч - на столько скорость велосипедиста на обратном пути больше, чем скорость на пути из города А в город В,
7 часов - время остановки велосипедиста (это время он не ехал)
5. Ещё раз читаем вопрос задачи.
6. Решаем, какую величину мы примем за неизвестное. Удобно принимать за неизвестное ту величину, которую надо узнать в задаче. В данном случае это скорость велосипедиста на пути из А в В.
Итак: пусть скорость велосипедиста на пути из А в В равна х. Тогда, поскольку скорость велосипедиста на обратном пути на 7 км/ч больше, чем скорость на пути из города А в город В, то она равна x+7.
7. Составляем уравнение. Для этого выразим третью величину уравнения движения (время) через первые две. Тогда:
- время, которое затратил велосипедист на дорогу из А в В равно 98/x,
- а на дорогу из В в А - 98/(x+7)+7 - вспомним, что на пути обратно велосипедист сделал остановку на 7 часов, то есть его время в пути складывается из времени движение и времени стоянки.
Уравнение составляем для времени. Ещё раз читаем в условии задачи, что в нем говорится о времени: В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. То есть время "туда " равно времени "обратно". Приравниваем время "туда" и время "обратно" Получим уравнение:
98/x=98/(x+7)+7.
Ещё раза проверяем размерность величин, которые входят в уравнение - нужно следить за тем, чтобы, например, не прибавлять к километрам часы.
8. Решаем уравнение. Теперь нужно сосредоточиться на решении уравнения. Для этого определим, какого типа это уравнение. Поскольку неизвестное находится в знаменателе дробей, это рациональное уравнение. Чтобы его решить, нужно перенести все слагаемые влево и привести дроби к общему знаменателю. Заметим, что числа 98 и 7 кратны 7.
Чтобы упростить решение, разделим обе части уравнения на 7. Получим уравнение: 14/x=14/(x+7)+1
После этого переносим все слагаемые влево, приводим к общему знаменателю, и приравниваем числитель к нулю.
Получаем в числителе: 14(x+7)-14x-x(x+7)=0 Раскроем скобки, приведем подобные слагаемые и решим квадратное уравнение.
Его корни: -14 и 7.
Число -14 не подходит по условию задачи: скорость должна быть положительной.
Ещё раз читаем вопрос задачи и соотносим его с величиной, которую мы нашли: за неизвестное мы приняли скорость велосипедиста на пути из А в В, и эту же величину требуется найти.
Ответ: 7 км/ч.
Как решать задачи. Итог
Заметим, что весь путь решения задачи мы разбили на маленькие кусочки, и на каждом участке сосредотачивались именно на обдумывании конкретного действия. И только после того, как это действие выполнялось, делали следующий шаг.
Когда не ясно что делать, нужно решить, какой маленький шаг можно сделать прямо сейчас, сделать его, а потом уже думать о следующем.
ege-ok.ru